Fairness metrics are crucial to how companies using AI measure their risk exposure to ML decision-making bias and AI compliance regulations to which they must adhere. While fairness and bias are very much in the eye of the beholder, the fairness metrics they rely on are pure math. Understanding the nuances of these fairness metrics is essential, as you must ensure that the metrics you monitor are aligned with the bias and regulatory risks your business is exposed to.
In this post, we will cover some common fairness metrics and their mathematical representations and explain the logic behind each to provide context on the suitability between fairness metrics and use cases.
Posts in this series:
- Making sense of bias in machine learning
- A gentle introduction to ML fairness metrics
- Dealing with machine learning bias
Basic fairness metric terminology
Before diving into the metrics, let’s align on some basic terminology and definitions commonly used under the bias and fairness context.
- Sensitive attribute: a.k.a. A “Protected field” is an attribute that may need to comply with a particular fairness metric. It’s important to note that not all attributes are sensitive by definition. Depending on the use case, only a certain subset of attributes with special consideration (legal, ethical, social, or personal) may be considered as such. For example, US federal law protects individuals from discrimination or harassment based on the following nine protected classes: sex (including sexual orientation and gender identity), race, age, disability, color, creed, national origin, religion, or genetic information (added in 2008).
- Proxy attribute: This means attributes that correlate to a sensitive attribute. For example, let’s assume that for a specific use case, race and ethnicity are sensitive attributes. The dataset may also contain highly correlated fields for these two. For example, an individual’s postal code might be highly correlated with them, making it a proxy attribute to the sensitive attribute value.
- Parity: A parity measure is a simple observational criterion that requires the evaluation metrics to be independent of the salient group 𝐴. Such measures are static and don’t take changing populations into account. If a parity criterion is satisfied, it does not mean that the algorithm is fair. These criteria are reasonable for surfacing potential inequities and are particularly useful in monitoring live decision-making systems (Source: Fairness and Algorithmic Decision Making).
- Confusion matrix: Fairness metrics are most commonly applied to classification use cases. One should be familiar with the basics of a confusion matrix to understand the basic mathematics behind the most common fairness metrics. In a binary classification case, we will refer to one of the predicted classes as “Positive” while the other will be “Negative.” Given this configuration, common performance metrics can be derived. To generalize for a multiclass classification use case, we refer to the sensitive class (meaning a specific value out of the possible classification classes) as positive, while all others are negative.
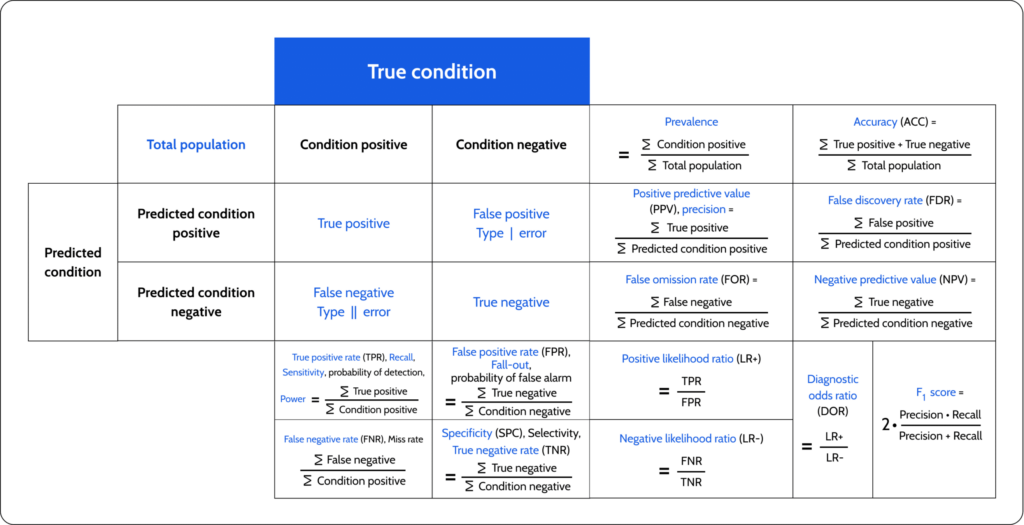
To view the complete list of possible metrics, see here.
Setup & notation
To illustrate fairness metrics in practice, we will use two real-life use cases of a loan approval process and an additional use case where the model attempts to predict the likelihood of an individual being convicted of criminal activity and sent to jail. A binary classification model predicts if we should give a positive answer, i.e., loan approval/going to jail, and the protected attribute, for our examples, will be gender.
Given this setup, we will use the following notation:
A – possible values of the sensitive attributes.
R – the output/prediction of the algorithm.
Y – the ground truth.
The graph illustrations of each example show the threshold of positive model outputs for each group, where every output above the threshold will indicate a positive outcome.
Metric 1: Group unawareness
Group unawareness means that we don’t want the gender of a person to impact in any way our decision to approve or reject a loan. In simple, intuitive words, we don’t want the model the “use” gender as an attribute. So if no requests from women make it into the pool of approved requests, that’s fair so long as requests are chosen purely based on non-sensitive attributes.
Group unawareness is a straightforward and intuitive way to define fairness. An ML equivalent term to such a condition could be feature attribution. When we refer to unawareness, we are technically referring to the fact that we want 0 attribution for gender attributes. This can easily be measured using tools like Lime, SHAP, etc.
Things to note
- There may be a “proxy sensitive attribute” in the data, which means attributes that correlate to a sensitive attribute. For example, an individual’s postal code may be a proxy for income, race, or ethnicity. So even if we willfully ignore the direct sensitive group, we may still have hidden awareness.
- The training data may contain historical biases. For example, women’s work histories are more likely to have gaps. Which may lower their requests’ probability of being approved
Metric 2: Demographic parity
If we want to ensure the same approval rate for male and female applicants, we can use demographic parity. Demographic parity states that the proportion of each segment of a protected class (e.g., gender) should receive a positive outcome at equal rates.
Let’s say A is a protected class (in our case, sex):
For 
Or
Another way to look at it is to require that the prediction be statistically independent of the protected attribute.
For all 
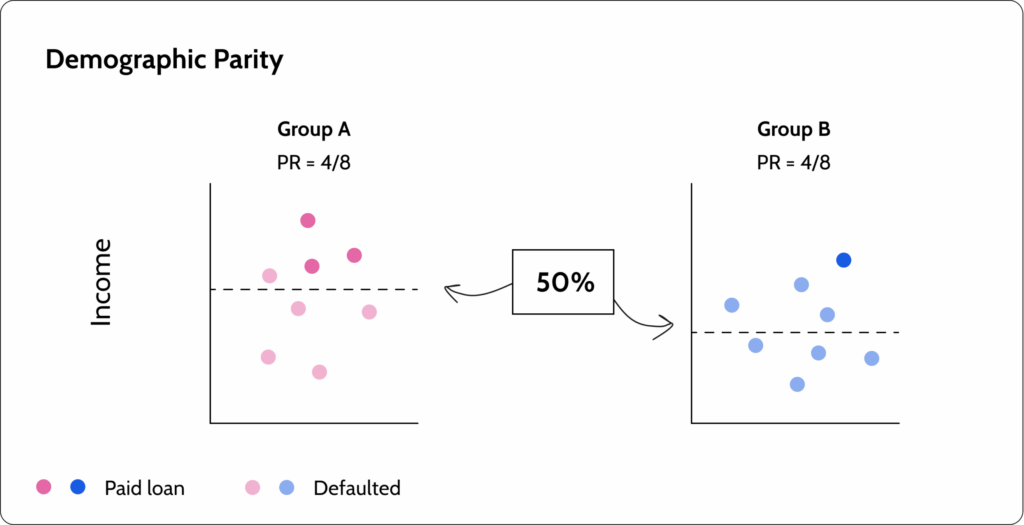
In this illustration, we can see that half of each group is approved.
Metric 2.1: Disparate impact
Disparate impact is a variation of demographic parity. The calculation is the same as demographic parity, but instead of aiming for an equal approval rate, it aims to achieve a higher-than-specified ratio. It is commonly used when some privileged group is in play (a group that has a higher probability of getting a positive answer when there is no fairness problem). For example, let’s say that people with high incomes have a higher likelihood of returning the loan. On the face of things, it’s OK for this group to have a higher approval rate than people with low income.
On the flip side, we want to ensure that the approval ratio between these groups does not become too high. The industry standard here is a four-fifths rule. If the unprivileged group receives a positive outcome of less than 80% of the proportion of the privileged group, this is a disparate impact violation. However, depending on your use case and business, you may decide to increase this.
The math
Things to note
Enforcing a specific ratio between groups may result in very qualified applicants not being approved or applicants with a low probability of returning the loan to be approved in the name of maintaining the ratio.
Metric 3: Equal opportunity
Equal opportunity examines the true positive rate (TPR). Meaning it looks at the number of people that returned the loan to see the ratio of them that the model approved.
The math
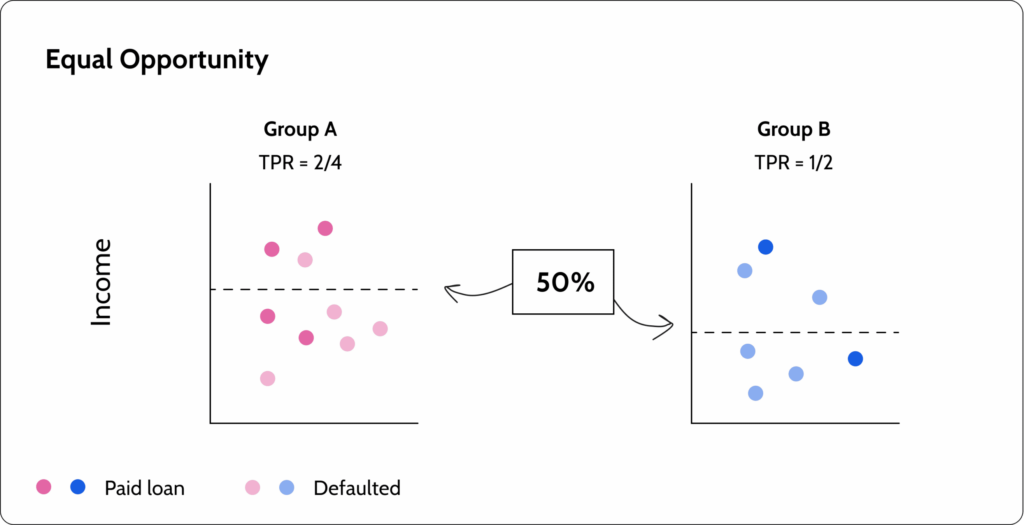
In the illustration above, we can see that both groups have the same TPR. Meaning that we are basing our fairness calculation on the actual, not the prediction output. This helps us mitigate some of the overbalancing risks inherent to demographic parity.
Things to note
It may not help close an existing gap between two groups:
Let’s look at a model that predicts applicants who qualify for a job. Let’s say Group A has 100 applicants, and 58 are qualified. Group B also has 100 applicants, but only 2 are qualified. If the company decides it needs 30 applicants, the model will offer 29 applicants from Group A, and only 1 from Group B as the TPR for both groups is ½ (29/58 = ½).
Metric 4: Equal odds
To understand why equal opportunity is not good enough in some cases, let’s look at a use case where we have a model that predicts if someone is a criminal where the protected attribute is race. Based on equal opportunity, the ratio of criminals that go to jail is equal between two ethnicities (see image below). However, we see that the FPR between the groups is different. The implication is that more innocent people from a specific sensitive group are sent to jail. In cases where we want to enforce equal TPR and FPR, we will use equal odds.
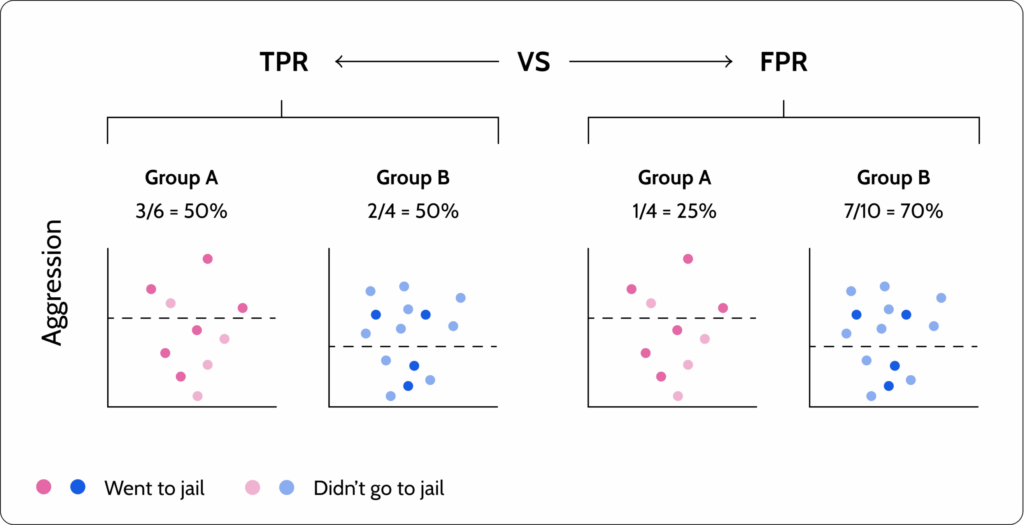
Equal odds is a more restrictive version of equal opportunity. In addition to looking at the TPR, it also looks at the FPR to find an equilibrium between them.
The math
![\[ \ P\left(R=+|Y=y,A=a\right)=P\left(R=+|Y=y,A=b\right),y\in\{+,-\},\forall{a,b}\in A}\]](https://superwise.ai/wp-content/ql-cache/quicklatex.com-b64335ea1a4da953645b7505b1a8662e_l3.png "Rendered by QuickLaTeX.com")
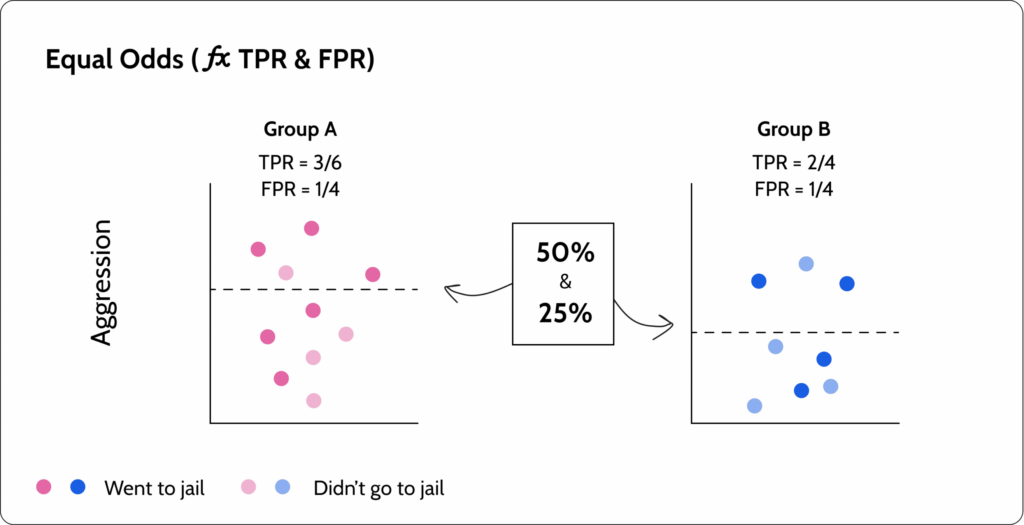
Things to note
Equal odds is a very restrictive metric because it tries to achieve equal TPR and FPR for each group. Therefore, it may cause the model to have poor performance.
Metric 5: PPV-parity
PPV-parity (positive predicted value) equalizes the chance of success, given a positive prediction. In our example, we ensure that the ratio of people that actually return the loan out of all the people the model approved is the same in both groups. Meaning we want to see that the two groups have the same positive predicted value (PPV).
The math
![\[ \ P\left(Y=+|R=+,A=a\right)=P\left(Y=+|R=+,A=b\right) \forall{a,b}\in A}\]](https://superwise.ai/wp-content/ql-cache/quicklatex.com-6372e2097b1616f29e9ab56969223dbe_l3.png "Rendered by QuickLaTeX.com")
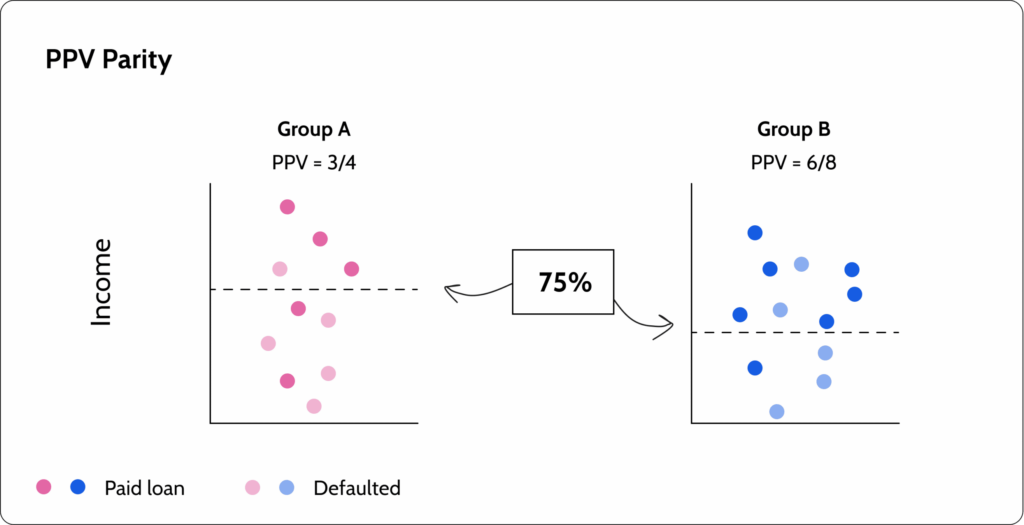
Metric 6: FPR-parity
FPR-parity (false positive rate) is the exact opposite. It wants to ensure that the two groups have the same false positive rate (FPR). In our example, we ensure that the ratio of people that the model approved but defaulted on their loan out of all the people that defaulted on their loan is the same in both groups.
The math
![\[ \ P\left(R=+|Y=-,A=a\right)P\left(R=+|Y=-,A=b\right) \forall{a,b} \in A}\]](https://superwise.ai/wp-content/ql-cache/quicklatex.com-9ede91903076e367ae48c13f32c0fa89_l3.png "Rendered by QuickLaTeX.com")
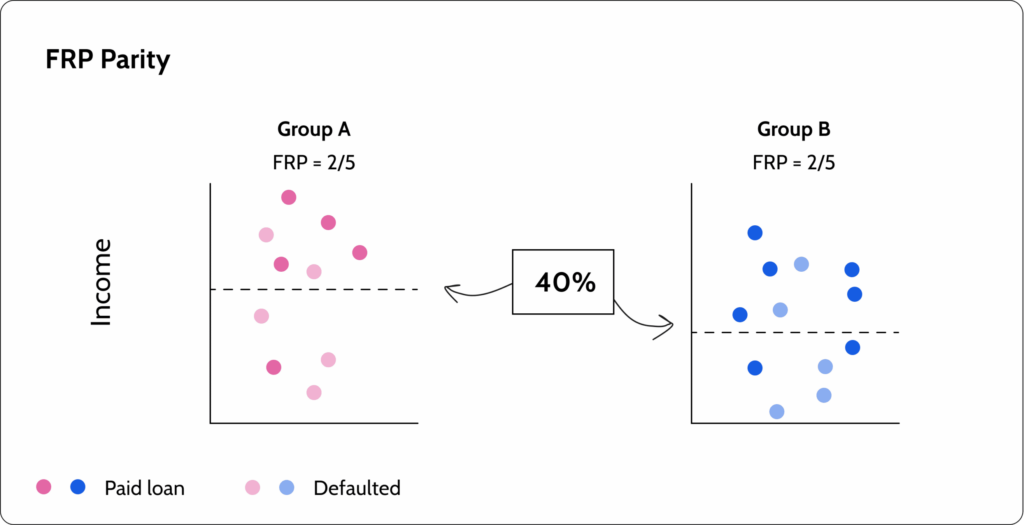
Metric 7: NPV-parity
NPV-parity (negative predicted value) says that we should ensure that the ratio of correctly rejecting people out of all the people the model has rejected is the same for each group. We want the two groups to have the same negative predicted value (NPV).
The math
![\[ \ P\left(R=-|Y=-,A=a\right)=P\left(R=-|Y=-,A=b\right) \forall{a,b}\in A}\]](https://superwise.ai/wp-content/ql-cache/quicklatex.com-d9d34c575378d0779ecca545f3e0bed5_l3.png "Rendered by QuickLaTeX.com")
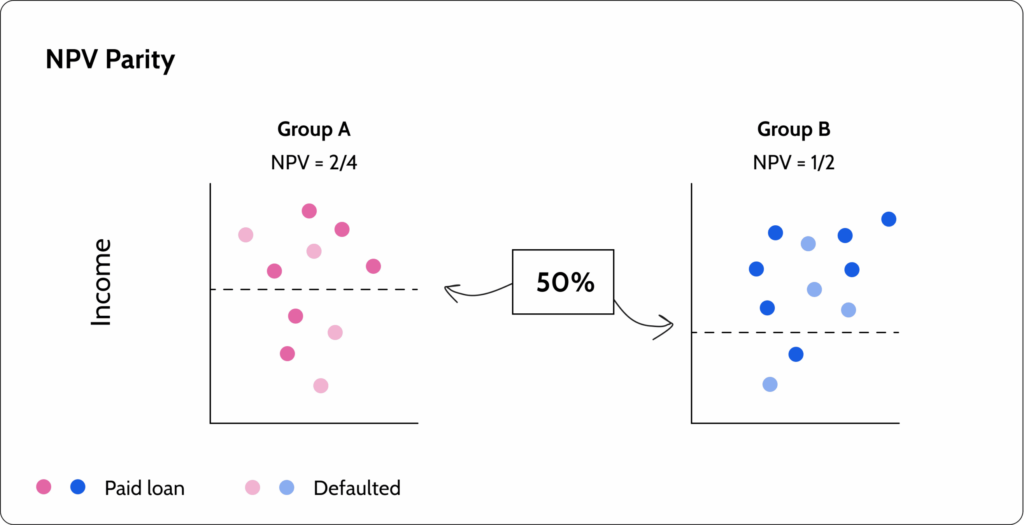
Open-source fairness metrics libraries
There are a variety of open-source libraries that can be used to measure fairness metrics and monitor bias. Here are a few common open-source libraries and tools of my choice from IBM’s book on AI Fairness.
| Open source library | Notes |
| AIF360 | Provides a comprehensive set of metrics for datasets and models to test for biases and algorithms to mitigate bias in datasets and models. |
| Fairness Measures | Provides several fairness metrics, including difference of means, disparate impact, and odds ratio. It also provides datasets, but some are not in the public domain and require explicit permission from the owners to access or use the data. |
| FairML | Provides an auditing tool for predictive models by quantifying the relative effects of various inputs on a model’s predictions, which can be used to assess the model’s fairness. |
| FairTest | Checks for associations between predicted labels and protected attributes. The methodology also provides a way to identify regions of the input space where an algorithm might incur unusually high errors. This toolkit also includes a rich catalog of datasets |
| Aequitas | This is an auditing toolkit for data scientists as well as policymakers; it has a Python library and website where data can be uploaded for bias analysis. It offers several fairness metrics, including demographic, statistical parity, and disparate impact, along with a “fairness tree” to help users identify the correct metric to use for their particular situation. Aequitas’s license does not allow commercial use. |
| Themis | An open-source bias toolbox that automatically generates test suites to measure discrimination in decisions made by a predictive system. |
| Themis-ML | Provides fairness metrics, such as mean difference, some bias mitigation algorithms, additive counterfactually fair estimator, and reject option classification. |
| Fairness Comparison | Includes several bias detection metrics as well as bias mitigation methods, including disparate impact remover, prejudice remover, and two-Naive Bayes. Written primarily as a test bed to allow different bias metrics and algorithms to be compared in a consistent way, it also allows additional algorithms and datasets. |
A final word about fairness metrics
Fairness isn’t an absolute truth, especially in the context of ML. You must recognize that there are many different fairness metrics, some of which have an inherent tradeoff. Plainly, some of them just don’t know how to work together. Furthermore, fairness metrics are a business-driven constraint. What should be considered a protected field, and what fairness criteria to use should be driven by the business. Or, more precisely, the bias, compliance, and regulatory risks that your business is exposed to. To help you navigate what fairness metrics are correct for your use case and business, there is a great fairness decision tree by The University of Chicago that can help you decide what metrics to measure.
In this post, we reviewed the basics of fairness metrics. But it’s one thing to measure fairness, and it’s a whole different thing to monitor fairness in production and detect unwanted bias. In our next posts, we’ll dive into bias, practical considerations of fairness and bias in the real world, and how to monitor bias and fairness in production ML systems.
Want to monitor bias?
Head over to the Superwise platform and get started with bias monitoring for free with our community edition (3 free models!).
Prefer a demo?
Request a demo here and our team will setup a demo for you and your team!
Everything you need to know about AI direct to your inbox
Superwise Newsletter
Superwise needs the contact information you provide to us to contact you about our products and services. You may unsubscribe from these communications at any time. For information on how to unsubscribe, as well as our privacy practices and commitment to protecting your privacy, please review our privacy policy.
