Data drift detection basics

Drift in machine learning comes in many shapes and sizes. Although concept drift is the most widely discussed, data drift is the most frequent, also known as covariate shift. This post covers the basics of understanding, measuring, and monitoring data drift in ML systems.

Data drift occurs when the data your model is running on is different from that on which it was trained. Mathematically speaking, it means changes in the statistical distribution of the model inputs (i.e., P(X)). While this kind of change does not directly imply that the underlying pattern has changed (see our previous post on concept drift), it’s usually a good proxy indicator. Even if the patterns are stable, which means you don’t have concept drift on top of the data drift, your model is probably not optimal for its current environment, which has likely changed since the model was trained.

More posts in this series:

1. Everything you need to know about drift in machine learning
2. Data drift detection basics
3. Concept drift detection basics
4. A hands-on introduction to drift metrics
5. Common drift metrics
6. Troubleshooting model drift
7. Model-based techniques for drift monitoring

Examples of data drift

What do we mean by data drift? Say you have a bank that is using a binary classification model to predict the probability of a customer defaulting on a new loan request. Now, let’s say the bank’s marketing department launches a new, aggressive campaign to attract young students. Assuming the campaign is a success, it will lead to a different distribution in the type of customers asking for loans. Although the underlying reality of who is a good loan candidate and who isn’t has not changed, the bank’s classification model is no longer optimized for this new mix of user profiles.

As another example, let’s take a content publisher that has a machine learning model to classify sentiment analysis for readers’ feedback on news articles. If the publisher decides to try a different editorial policy that tends to create shorter articles, both the articles and the reader’s feedback will change. The original sentiment analysis model was not optimized for short articles and will start working differently once a greater portion of the articles are short.

Measuring data drift

Measuring data drift is not straightforward. There are two main aspects to defining the right drift metrics. First, you need to understand which distribution you want to test and check if it’s drifting relative to the distribution you choose as your reference distribution. Second, you’ll need to decide how to quantify the distance between these two distributions.

Defining the tested period and the reference distribution

Measuring drift usually implies having a tested distribution that is drifting from a given reference distribution. What we should consider as the tested period and what we should consider as the reference distribution for comparison should be customized on a case-by-case basis.

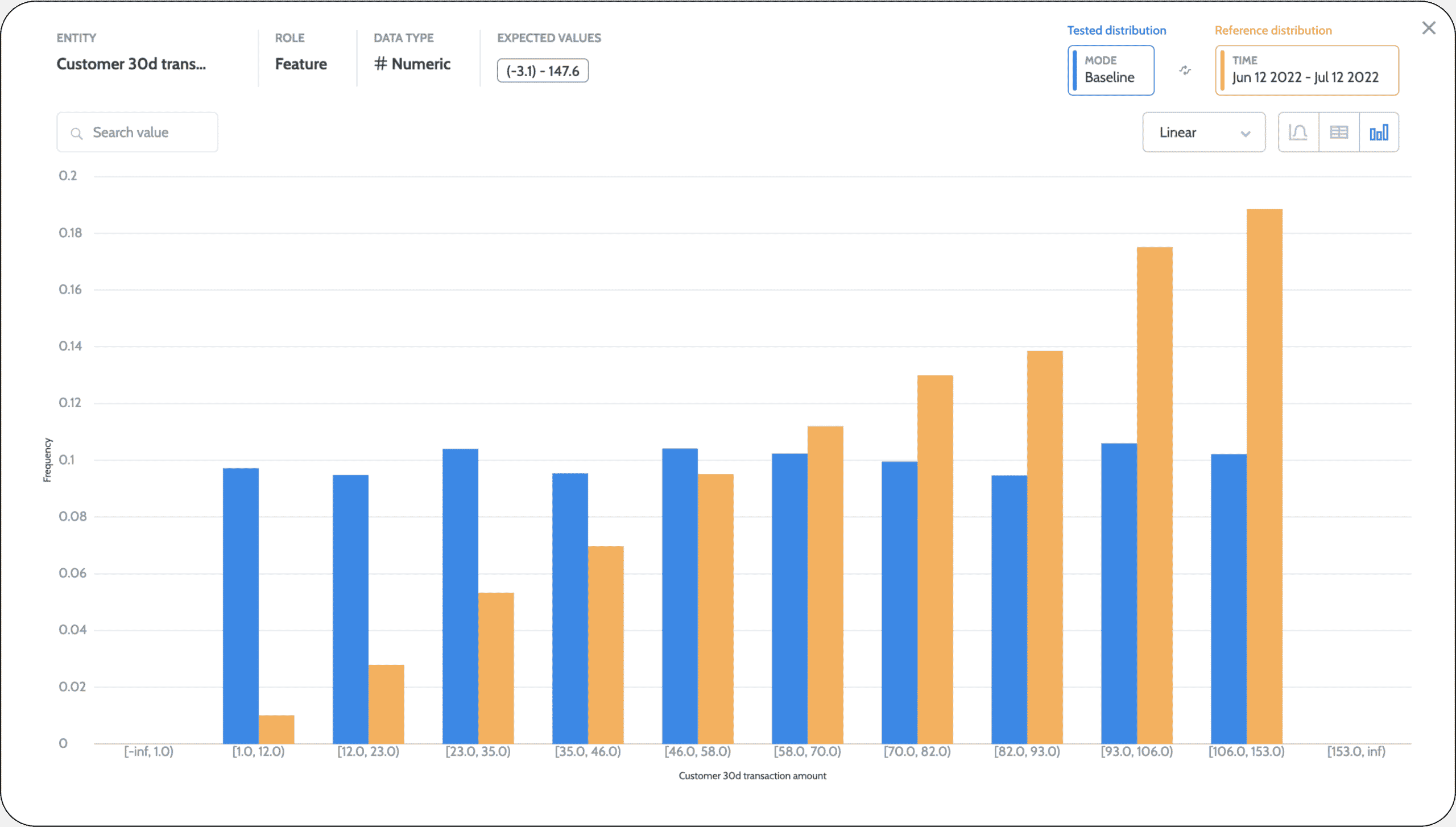
The tested distribution

In operational systems, we generally use a sliding window to compare and test our distribution over time. The big question is what time resolution to use: the last minute, last day, week, or month? Defining a shorter time resolution enables you to capture drift cases faster but also has the potential to be significantly noisier. Besides, even if you detect a drift in the last few minutes, you won’t necessarily have all the information needed to act on it and resolve the issue. You’ll need clear evidence over time to decide if you want to retrain the model. It’s best not to jump to conclusions before you are confident of the resolution required.

Defining the reference distribution

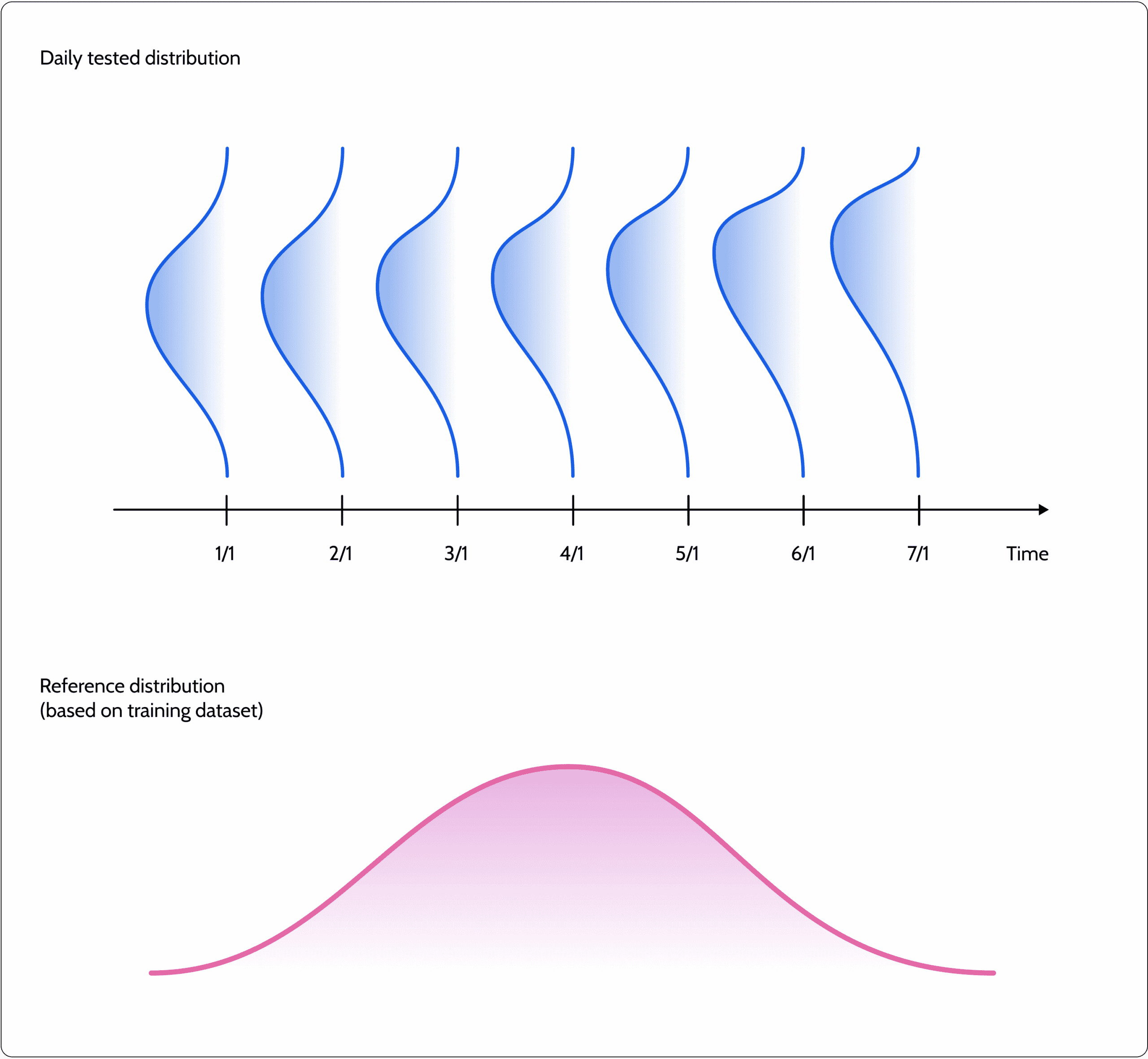
The most common use case for drift is to test for a training-serving skew. This means detecting whether the model in production is working under different circumstances than what was assumed when it was being trained. Usually, this can also be referred to as a type of uncertainty measure. However, in many cases (e.g., imbalance use case), the training dataset may not reflect the real-life distribution. How does this happen? We may have rebalanced classes, run stratified sampling, or other normalization methods that can impact the training dataset’s representation of real-life distribution. In these cases, it may be better to compare your production distribution to the test dataset, which was untouched and represents the actual distributions assumed.

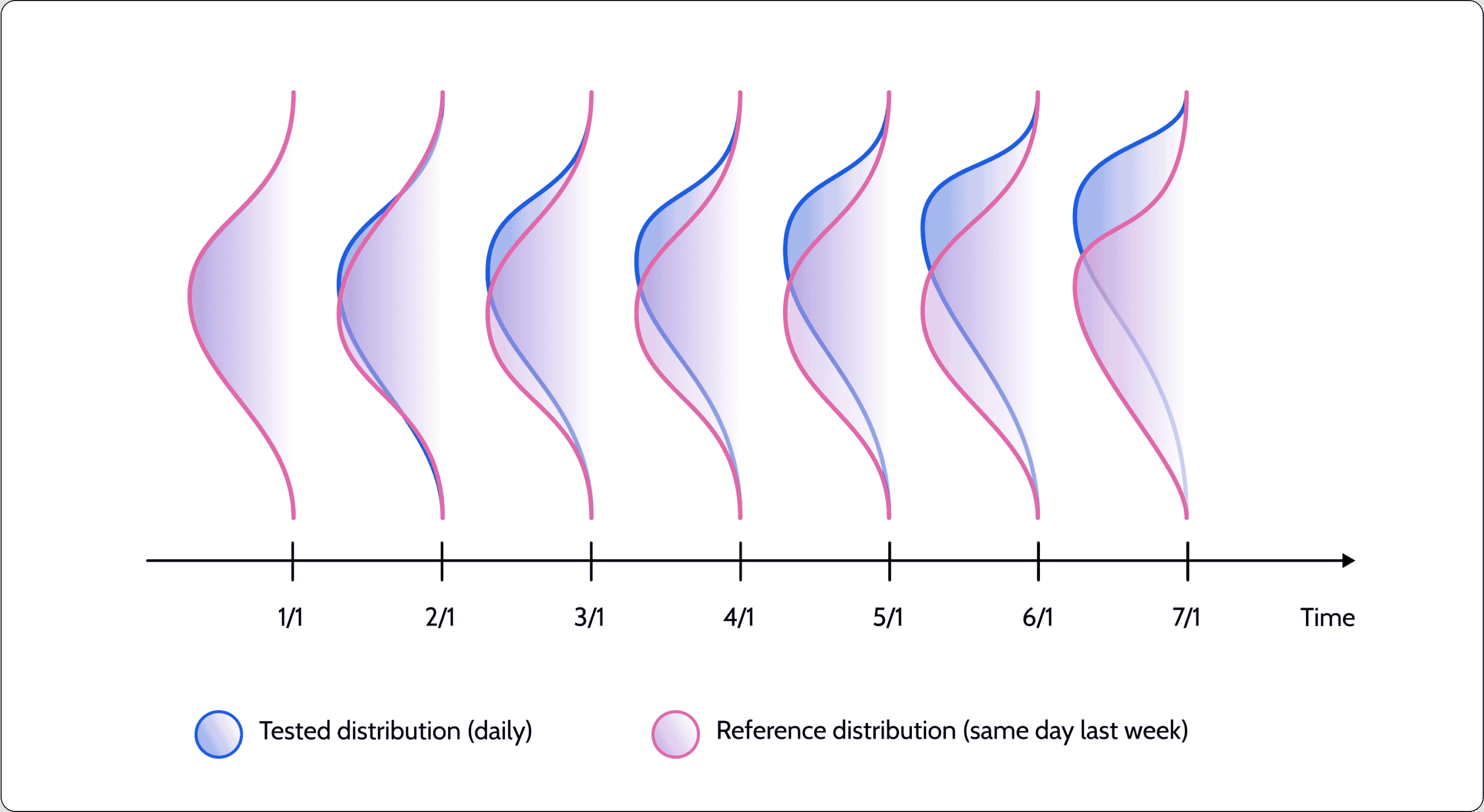
Another typical drift use case compares the tested distribution with a sliding window. For example, corresponding to a parallel day in the last week or even the previous month’s distribution. While this isn’t a good indication of the model’s uncertainty, it serves to highlight whether the underlying data distribution has been changing. It may be that the production distribution is actually becoming more similar to the original training dataset distribution but was very different from the distribution a week ago. Your knowledge of the use case and data should help you determine whether this is an anomaly or something completely normal. Using a sliding window reference distribution is very common in seasonality use cases, where we can test the tested distribution to the equivalent distribution a season ago.

Univariate vs. multivariate drift

Once you’ve decided what distribution you want to test and what reference distribution you want to compare it to, you need a mathematical function to help you quantify the drift. 

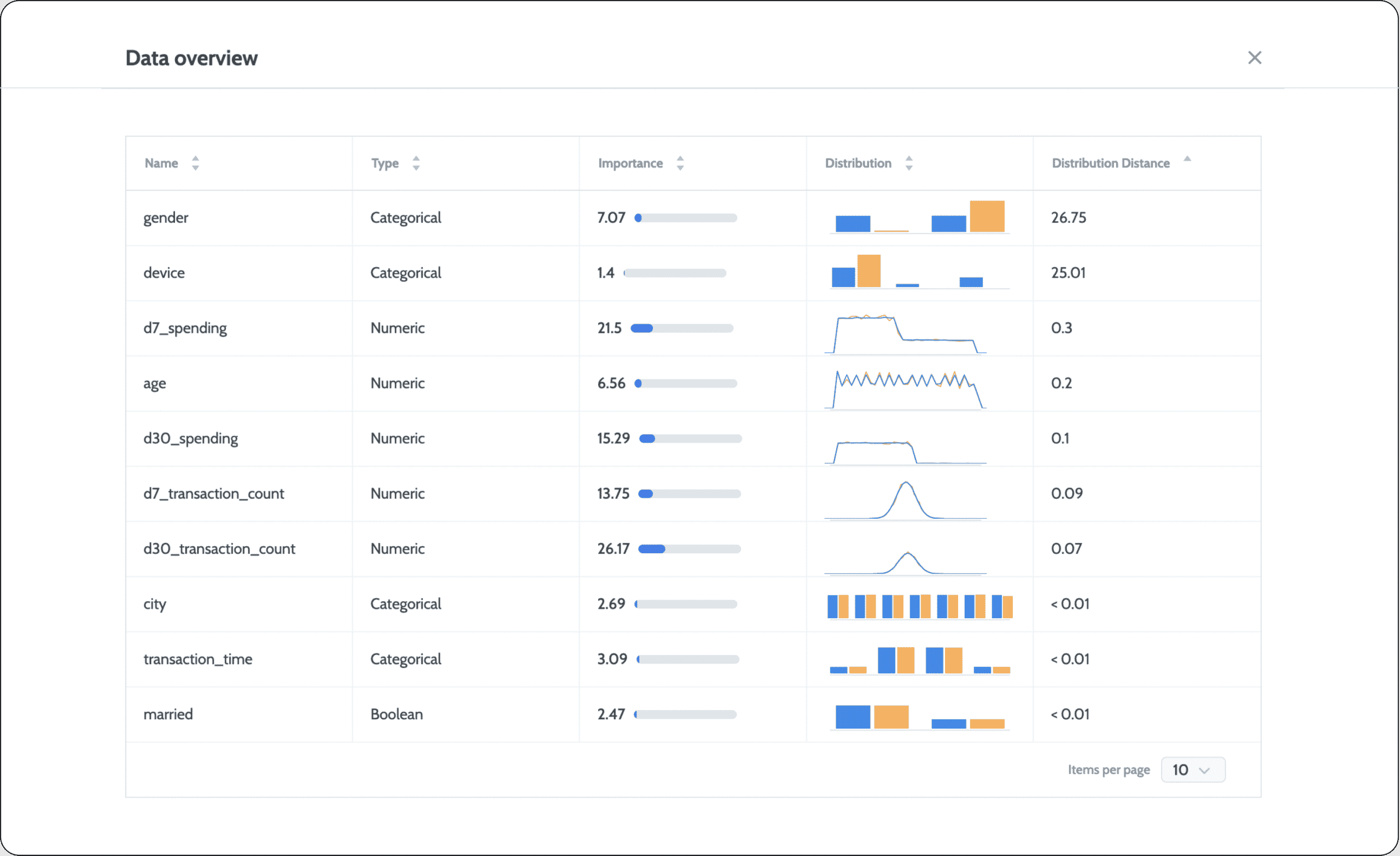
Many different statistical measures can be used to quantify the distance between the tested distribution and the reference distribution of a given feature. Each has its own properties, and some are model-based calculations. But, one of the key considerations for any type of quantification is how to incorporate drift into a single metric across the entire dataset. In short, you want to get one data drift score across all the features. Many machine learning models leverage dozens, hundreds, or even thousands of different features. In scenarios of high dimensionality, looking for drift only at the feature level will quickly lead to an overload of alerts due to the granularity of the measurement method. A common practice here is to quantify drift for the entire dataset together, a.k.a covariate drift. Once you see an indication of drift, you can drill down to understand precisely what is drifting and where it’s drifting.

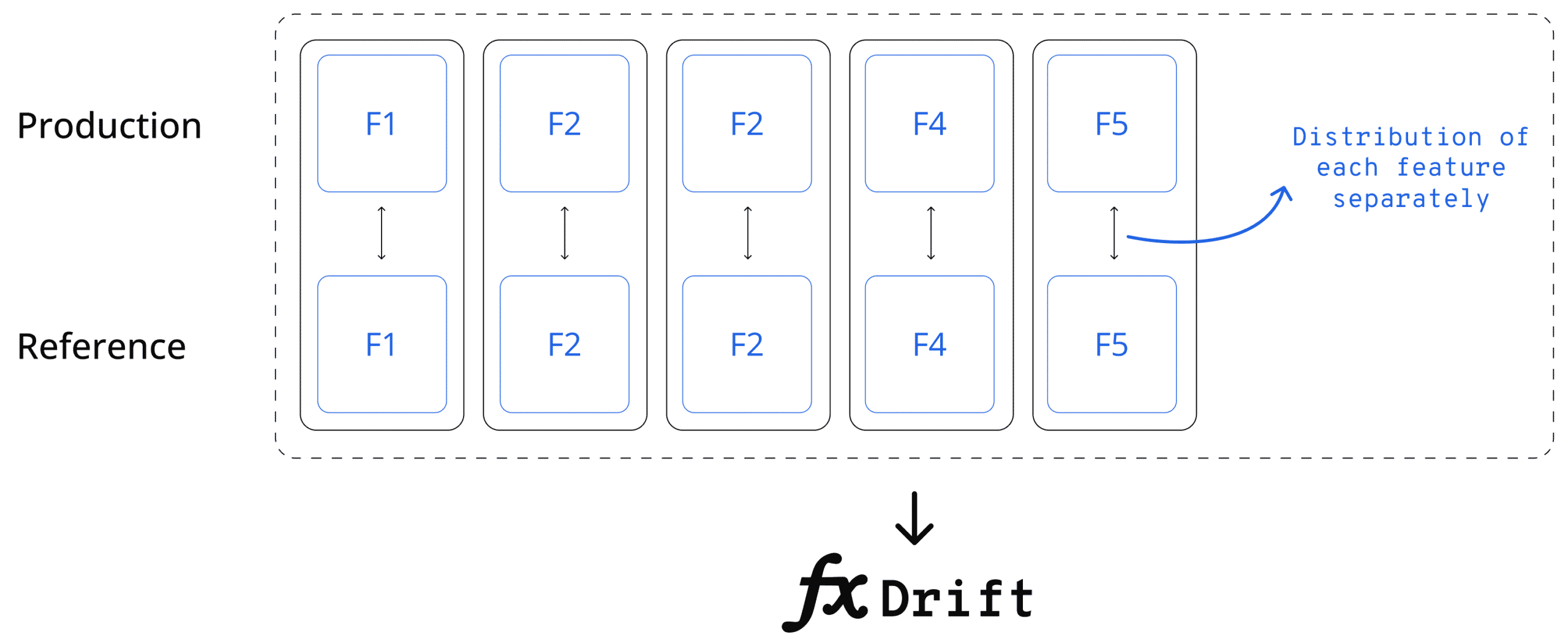
To quantify drift for the entire dataset, you can either compute the drift on a per-feature basis and then use some aggregation function to get a single aggregated drift metric. For example, you might compute the average drift level in all of the features to come up with a single score. You could even normalize this according to the importance of each feature (if available). Another option would be to leverage multivariate methods from the get-go. Below are some pros and cons of using the univariate approach.

Advantages of the univariate approach

• Simple to implement – You can choose from a variety of statistical measures that can be easily applied to a single univariate distribution.
• Easy to drill down to drifting feature/s and, therefore, easy to interpret. You can just drill down and see the drift score of each feature and decide how it contributed to the general drift score.
• It can easily be adjusted to weigh different features according to their importance.

How the univariate approach falls short

• It can be impacted by redundancy. For example, if you have three significantly correlated features, drift in all three will be measured and counted multiple times in the overall metric.
• It cannot capture multivariate drifts. Drift can happen in such a way that while each feature by itself has the same distribution, the conditional distribution of 2 or more features together is drifting.
• Not all quantification methods have the same scale. It can get complicated to average between different categorical and numerical features that use different types of quantification methods.

Monitoring data drift

Monitoring data drift introduces many challenges beyond the need to define and measure drift correctly for each use case. One main challenge is defining thresholds. In traditional monitoring, we generally know what thresholds to use for monitoring and when we want to be alerted based on our domain expertise. For example, you may want to receive an alert if CPU use goes above 80%. With drift, different quantification methods can create different scales of values, and there is no clear definition for what constitutes a “bad” drift level. The general consensus is that the bigger the drift, the bigger the change, and the higher the chances we need to be notified. What makes the most sense when it comes to data drift is to measure the tested data drift and set thresholds–whether manual or dynamic–that are based on monitoring what goes above or below normal behavior over time.

Summary

While not all data drift will necessarily impact the performance of the process, it’s usually a good indicator that something isn’t working as expected or your model could be more optimized for the real world. Measuring and monitoring data drift is an essential aspect of any model monitoring activity. Which distributions you want to compare and what types of measures you should use require a deep understanding of your specific use case and business. Your ML observability platform should give you the flexibility to pick and choose between them all.

In our next posts on drift, we’ll take a deeper dive into common statistical and model-based metrics for measuring drift and best practices for handling drift once it is detected.

Want to monitor drift?

Head over to the Superwise platform and get started with drift monitoring for free with our community edition (3 free models!). 

Prefer a demo?

Request a demo and our team will show what Superwise can do for your ML and business.