Drift is one of the top priorities and concerns of data scientists and machine learning engineers. Yet while much has been said about the different types of drift and the mathematics behind the methods to quantify drift, we are still left with the question of how to decide what metric or metrics best fit our models and use cases. And this is the crux of the matter – there are no absolute answers here.
Instead of focusing on theoretical concepts, this post will explore drift through a hands-on experiment of drift calculations and visualizations. The experiment will help you grasp how the different drift metrics quantify and understand the basic properties of these measures.
More posts in this series:
- Everything you need to know about drift in machine learning
- Data drift detection basics
- Concept drift detection basics
- A hands-on introduction to drift metrics
- Common drift metrics
- Troubleshooting model drift
- Model-based techniques for drift monitoring
Quantifying drift metrics
Models train on a finite sample dataset that has some statistical characteristics. There may be cases your model has not observed, specific cases it has observed but does not scale well too, be true to only some of the population, and maybe, after extrinsic changes, the data may just be irrelevant. Therefore, you need a way to detect when the data you are predicting on is vastly different from the data you modeled with during the training phase. For example, to measure training-serving skew, you should define the relevant, tested period and reference distribution to measure drift. To understand how different distance metrics can impact drift measurements under various scenarios, you can dive into the theoretical nuances of each drift metric type. However, we thought a more tangible (and fun) approach would be to run an example experiment that empirically visualizes some of the primary differences between the different drift metrics.
The following sections will review the experiment configuration, the raw results, and the key observations. The entire experiment is reproducible via our notebook.
The experiment
- Generate samples from a few different distribution families. Normal, uniform, and lognormal for continuous distributions and multinomial for discrete.
- For each class, instantiate a few different distribution samples representing the selected distribution class with selected parameters (for simplicity, we only selected mean and variance) and calculate drift through different measures between each pair of these samples.
- Note on naming convention: We named the samples according to their distribution parameters with the following naming convention.
<distribution_name>_<mean>_<variance> , e.g. normal_0_2. - Additionally, we named multinomial samples:
- Cat_uniform_k – where the values are 0 to k-1 with equal probability.
- cat_tilted_<mid/right/left> – where values are between 0 to 6 s.t.
- Probabilities are equal except for the median/max/min value, which has a higher probability.
- Note on sample size: We generated 1,000 samples for each distribution.
- Note on naming convention: We named the samples according to their distribution parameters with the following naming convention.
- For each sample1 (we will use a short version “s1”) and sample2 (“s2”), we calculated drift by comparing the two distributions with 7 different distance metrics: PSI bins and PSI quantiles (calculating the same metric with 2 different binning strategies), Chi-Square, Wasserstein, Kolmogorov-Smirnov (KS), Kullback–Leibler (KL) and, Jensen Shannon (JSD). We computed the same measures for continuous/numeric samples and categorical/discrete features, not because you should always use all these measures together but to emphasize their weak/strong points. In the example notebook, we made assumptions on how we drew these observations so we could use them as numeric features with mostly the same repeating values for the comparison to be feasible.
- Visualize and analyze the different results.
- Repeat the same calculations using only normal distributions to visualize known distribution parameters affecting different drifts.
Results
The raw output of our example experiment is the following table split between numerical and categorical features. Each row describes the measurement of different distance metrics between 2 selected distribution samples. Because some distance metrics are not symmetric (as evident in our results), each test contains the two forms of (s1, s2) and (s2,s1).
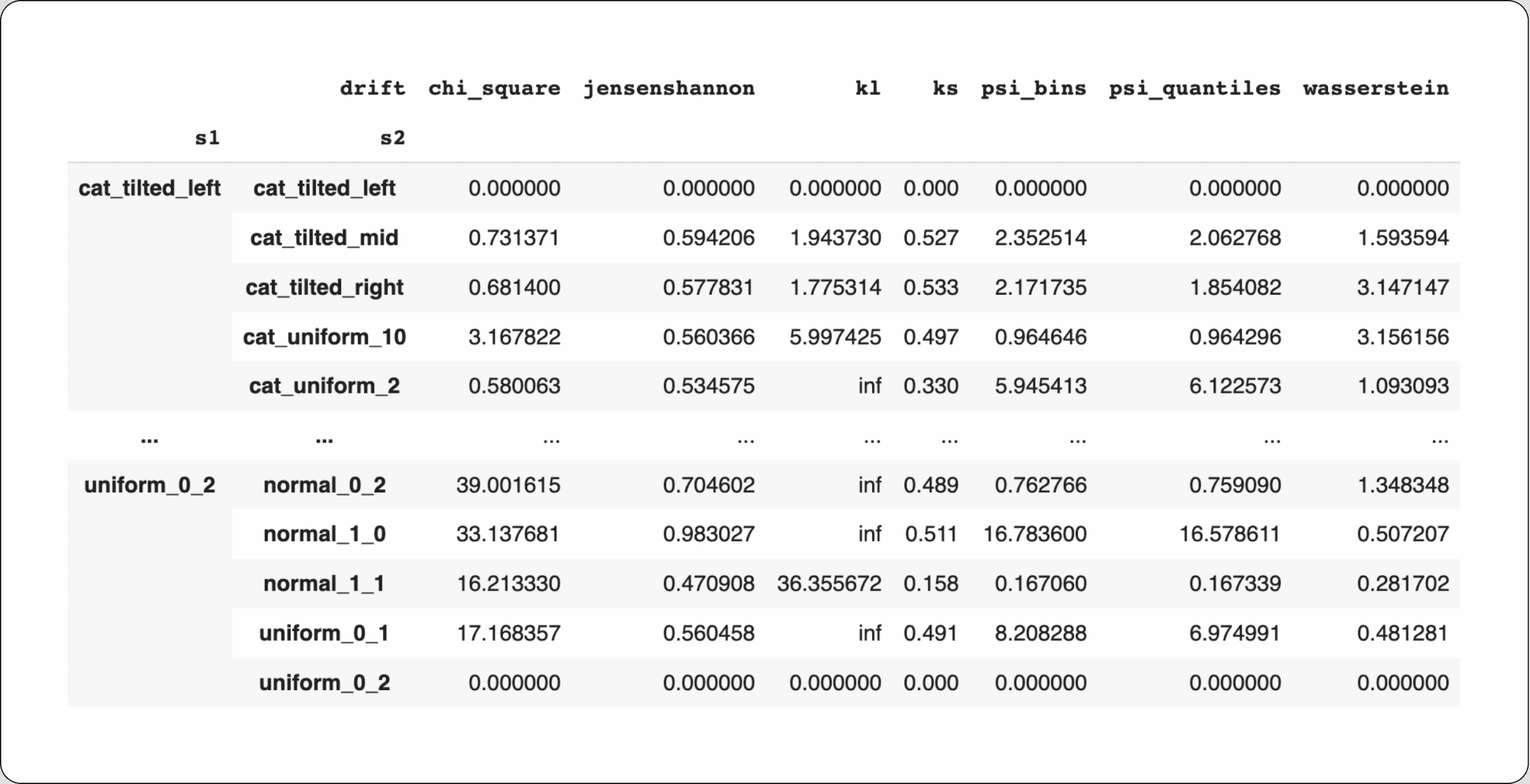
Insights
1 – Each metric has its own scale
While some metrics, like JS, have closed boundaries, others, like KL, don’t. This means that you cannot use different metrics on different features if you want to have an interpretable comparison between them. For example, if you used KL for feature 1 and Wasserstein for feature 2, you cannot compare which feature is drifting the most because the magnitudes aren’t aligned.
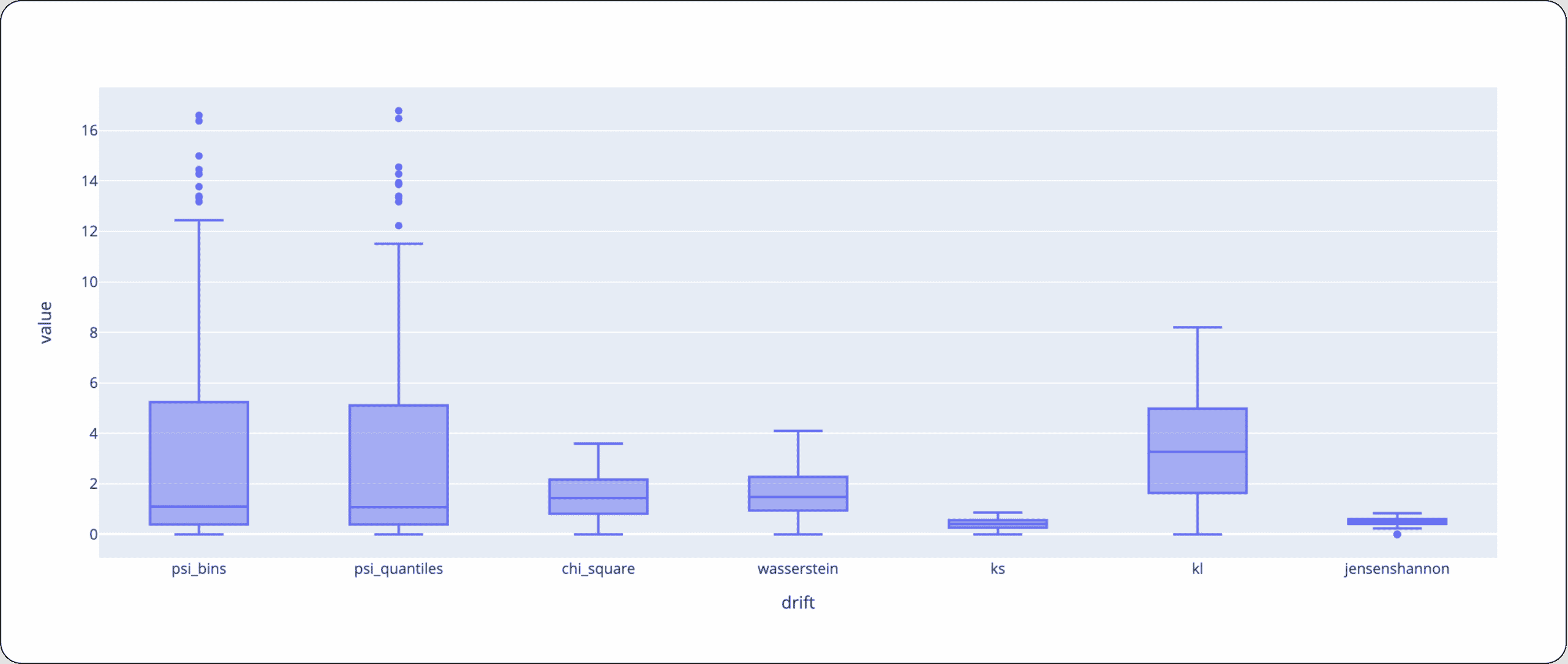
2 – Different metrics are relevant to different types of features
Wasserstein distance can’t be computed for categorical/discrete distributions because it assumes that distance between bins exists, which means that changing the order of bins will result in unwanted change in drift. On the flip side, Chi-Square/ KL/ JSD/ PSI don’t utilize distance between bins, which means that while drastic changes in the distribution may have occurred, you won’t encapsulate it in terms of “how far” they’ve moved or changed the distributions.
Consider the following distributions with the values 0 through 6. One distribution is tilted toward the center, while the other two are tilted towards the right and left sides.
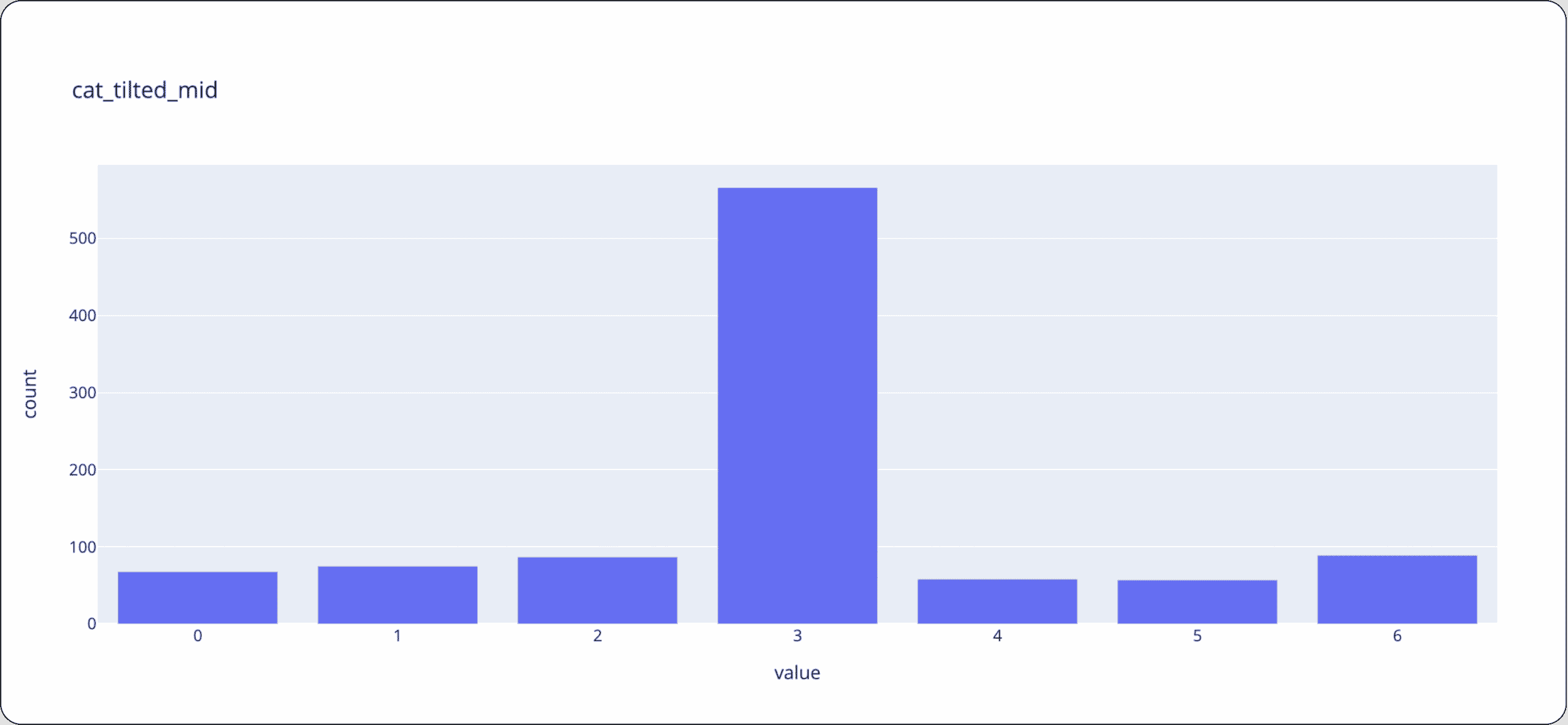
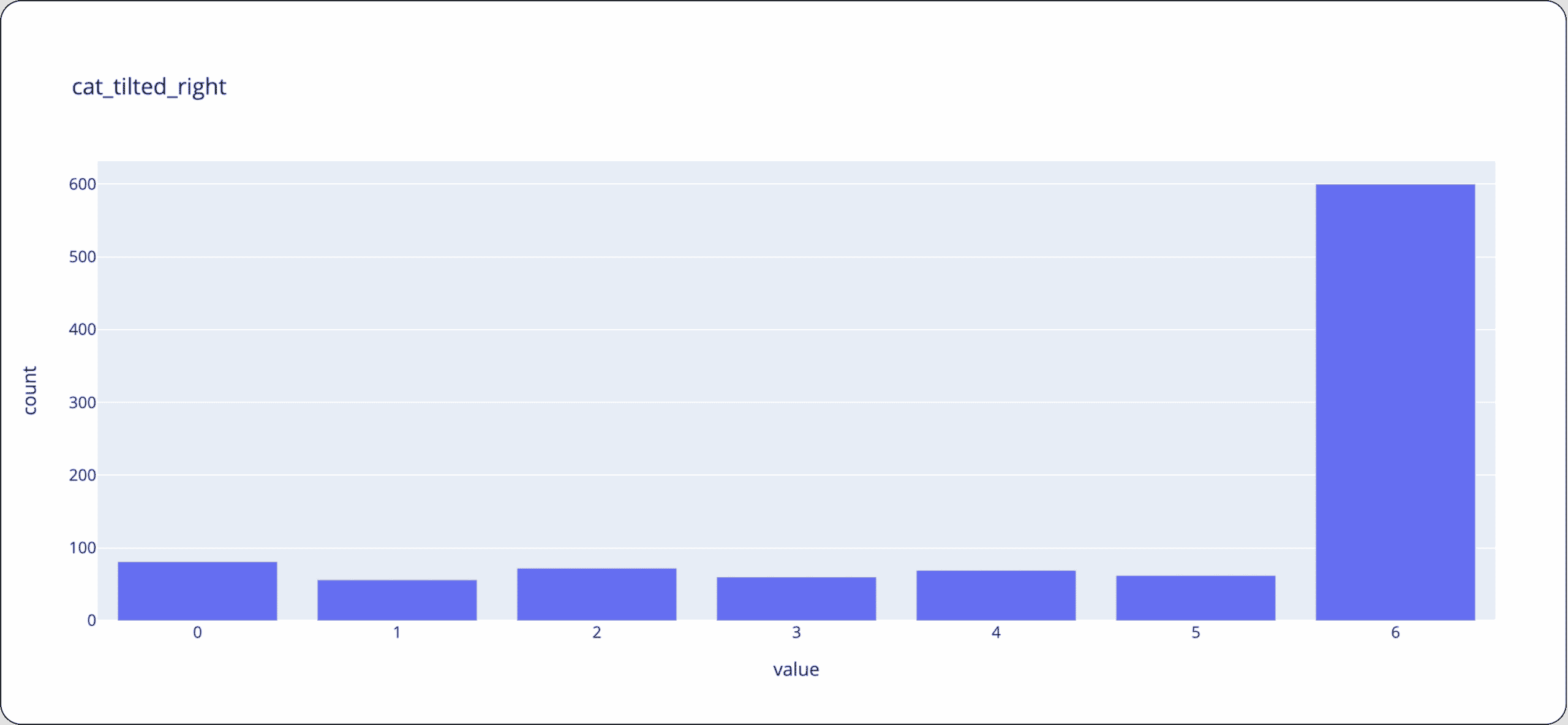
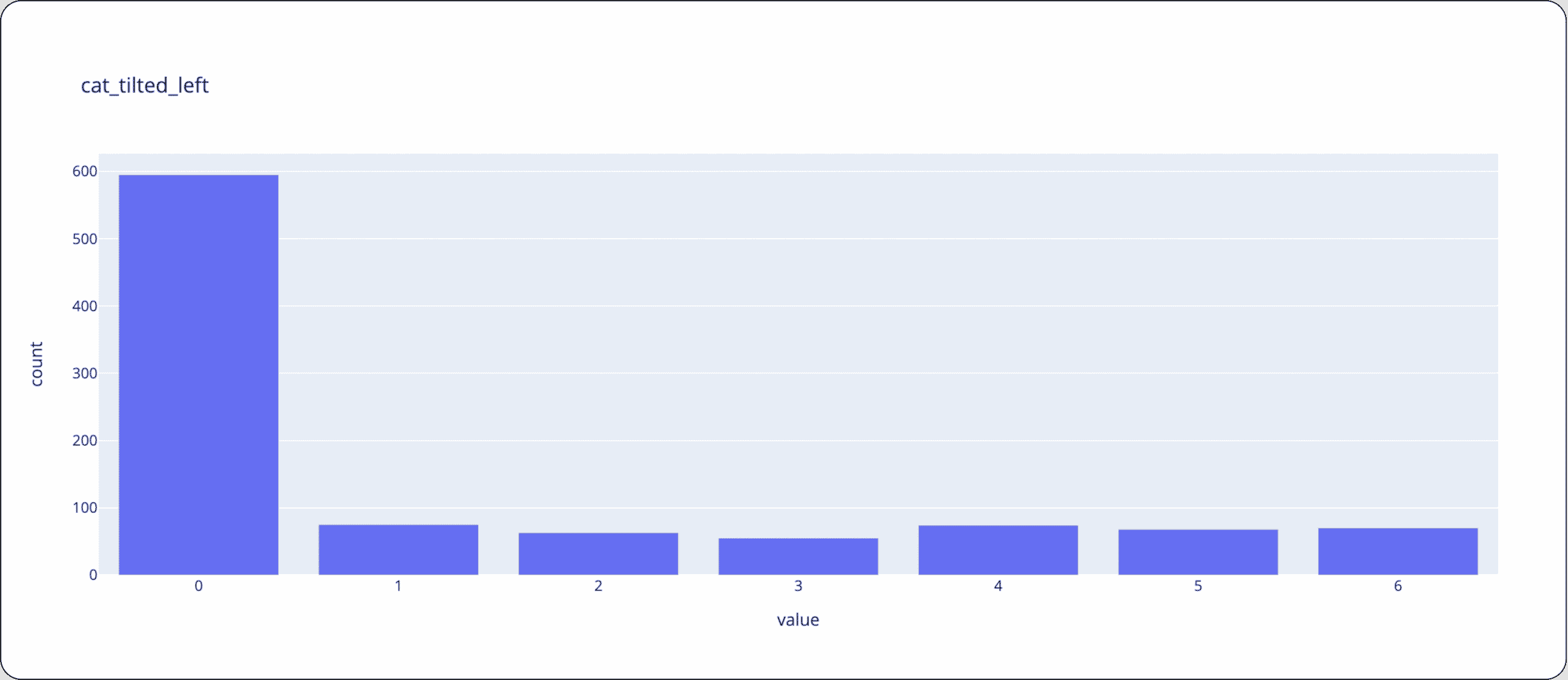
Let’s drill into the details and look at the different drift calculations between these samples. Notice how the Wasserstein distance between the center distribution and the right and left distributions are roughly the same (~1.59) and is larger than the tilted right and left distributions (~3.14). However, Chi-Square stays approximately the same between all comparisons (except in asymmetry change) as it doesn’t take into account the distance between bins or where the data has shifted. Therefore KL and JSD are more suited to categorical or spare numeric features (where the distance between different values has no meaning).

3 – Some metrics are more similar to others
Understanding which distance metrics correlate and which do not under the same distribution comparison modes could give us a simplified view of which distance metrics have similar characteristics and which could behave very differently under different scenarios. To do so, we ran a correlation matrix analysis on top of our raw results to examine which distance metric combinations are highly correlated and which are not.
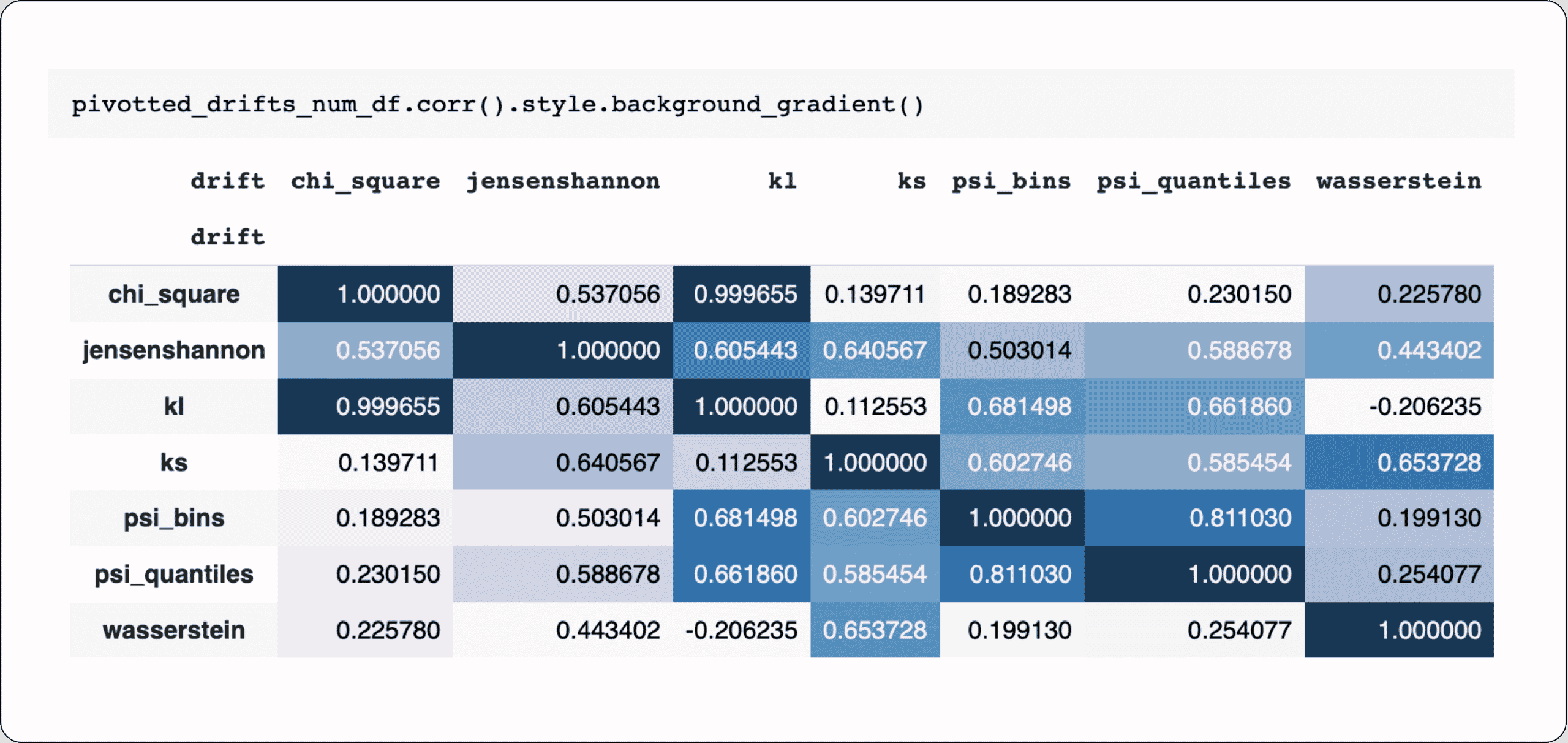
Looking at the correlation matrices results above, we can observe:
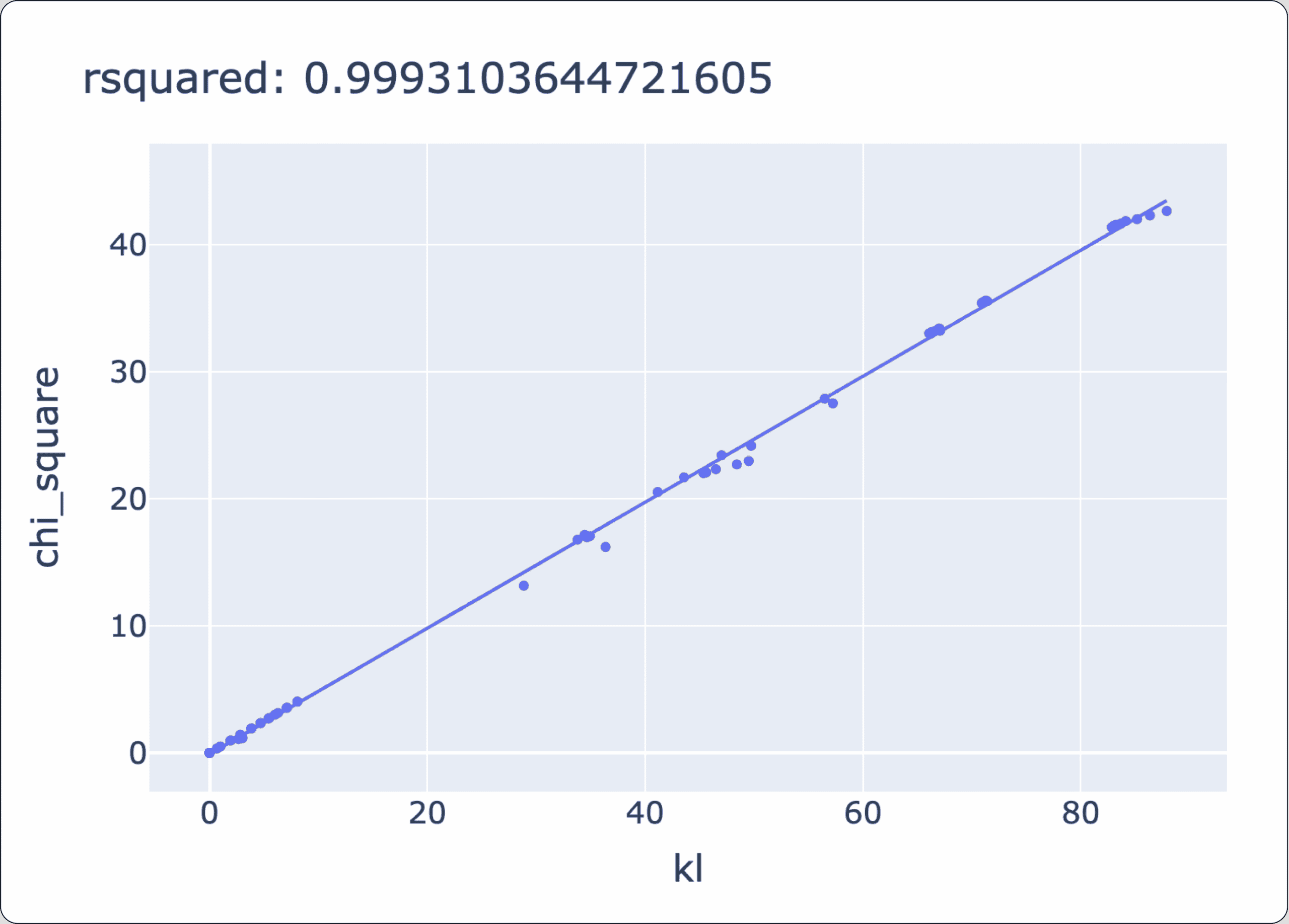
- In our experiment, KL and Chi-Square are strongly linearly correlated.
- Wasserstein is not linearly correlated to most metrics except KS, which is expected to be similar (Wasserstein is the sum of diffs of the CDF, and KS is the SUP/max distance between the CDFs).
- Wasserstein and KS are correlative in all cases (as expected).
- KL, in all cases, correlates with JSD (as expected), which we can see in the scatter plot below. This makes sense because when we look at their mathematical definition (see common drift metrics), we see JSD is derived from KL (while each one has its own scale).
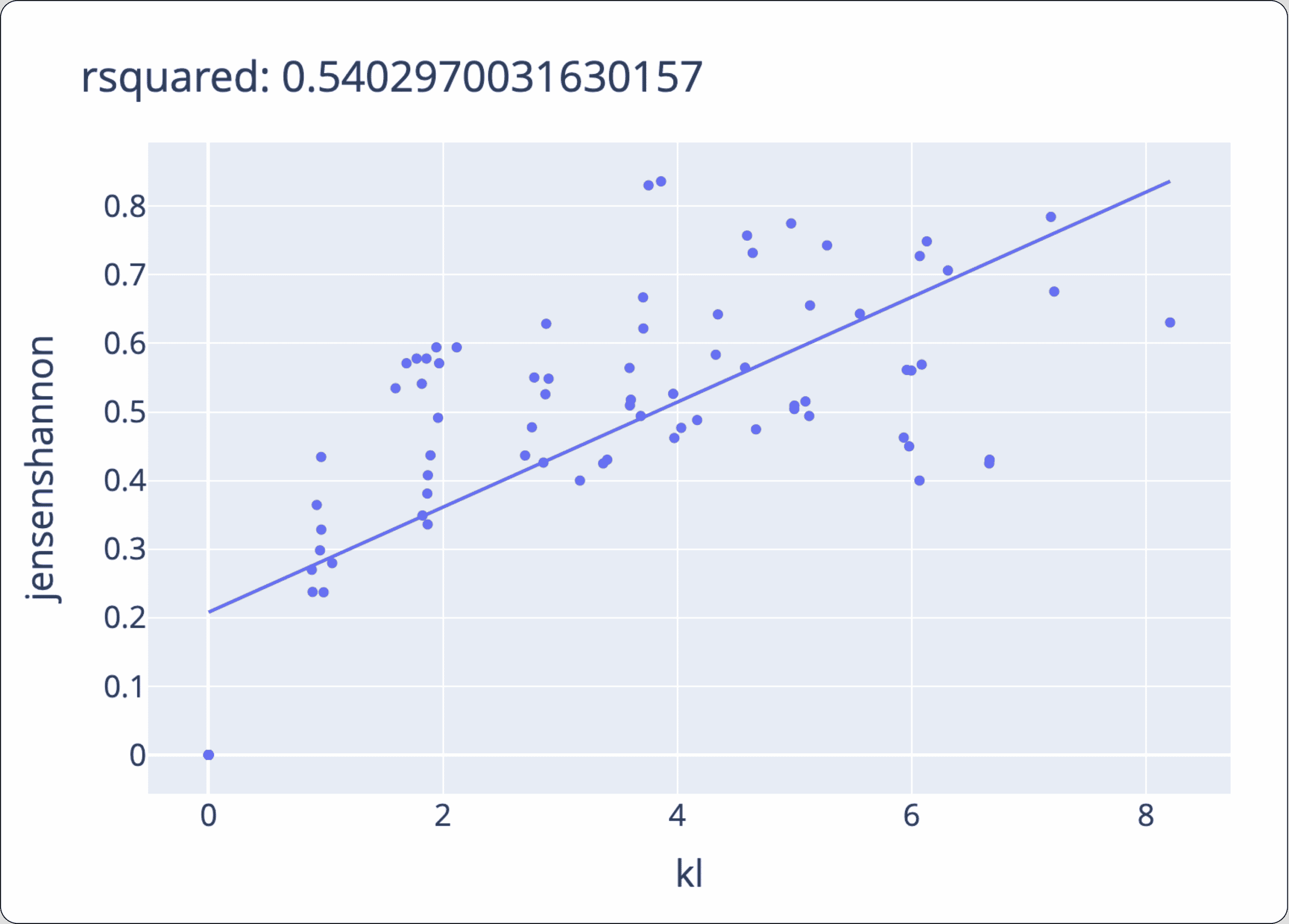
4 – Binning strategy can alter the results
* Tested only on PSI
For most distance metric implementations, we need a binning strategy. The binning strategy will get the estimated density of the statistical methods to use when comparing PDF. The computations of many measures rely on an estimated distribution/histogram from our sample data, and you need the bins to remain the same to compare samples. The binning strategy will result in different distribution sampling, so it can majorly affect results in a lot of these methods.
To better visualize the effects of changing the binning strategy, the following sample bins example shows what happens when we use them to sample other distributions (code available in the notebook under “Binning Strategies”).
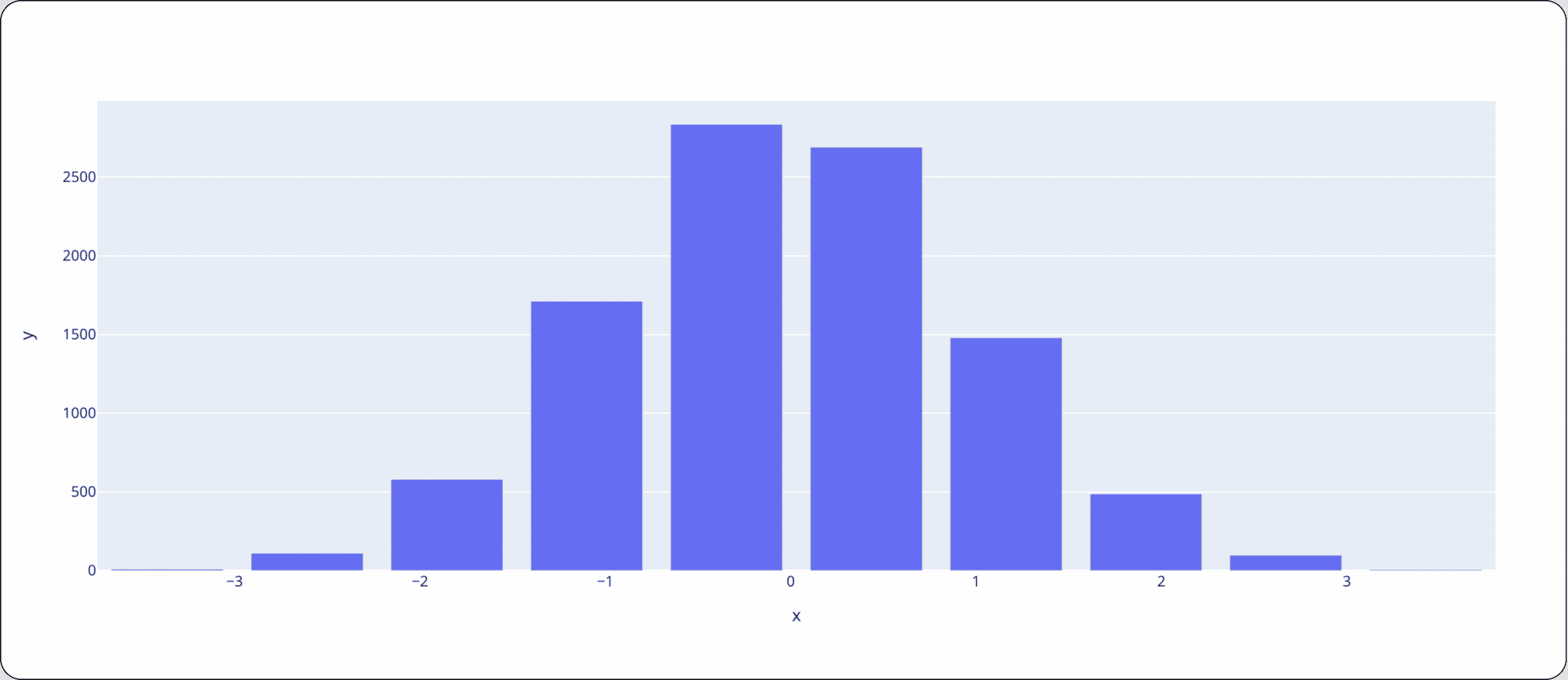
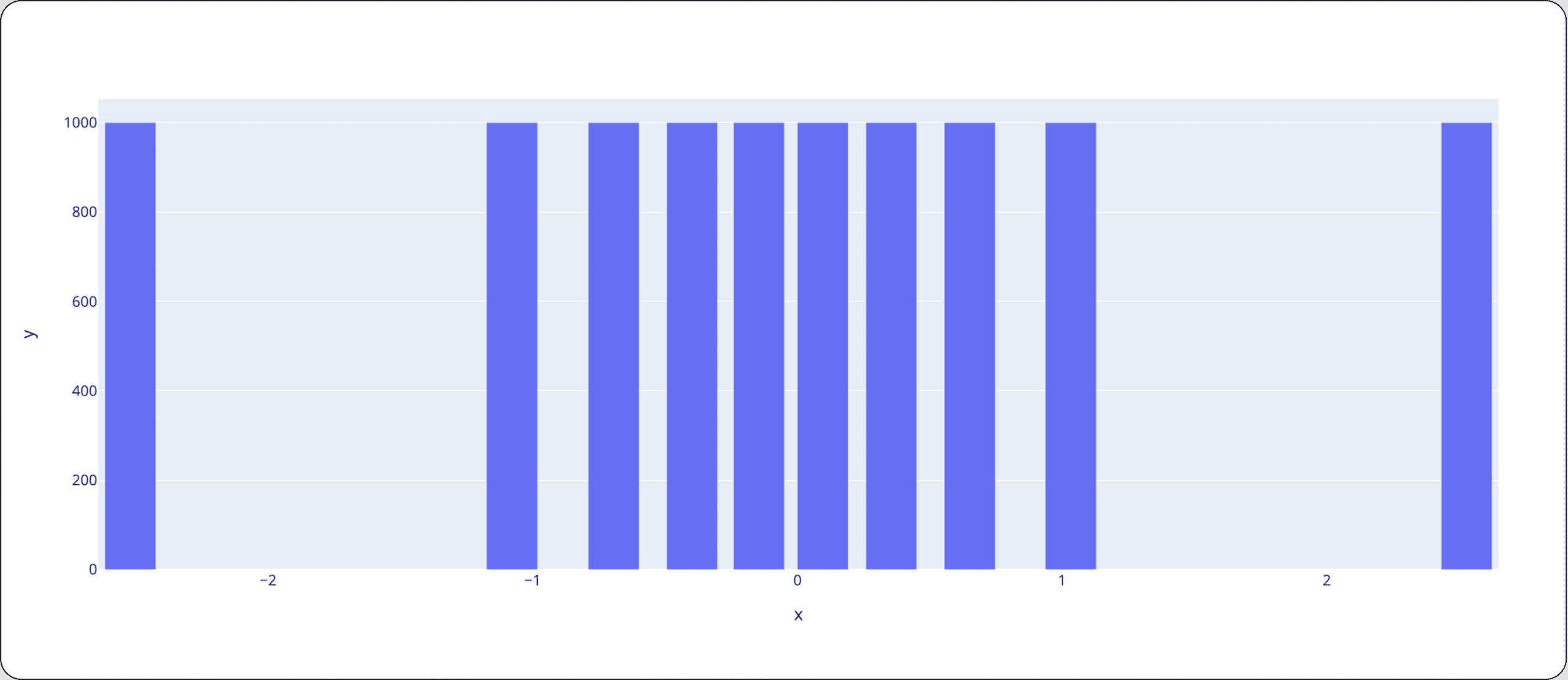
10 bins where each bin represents a percentile, meaning that the first bin on the left has the smallest 10 percent of the data, the second bin has 10 percent of the data, s.t. It is bigger than the left bin and smaller than 80% of the data, and so forth.
*Note the distribution shown above is normal, centered around 0 with a variance of 1. Using the bins/breakpoints strategy above, let’s see how a different observed distribution will be measured differently. The distribution we’ve drawn is normal, centered around 1 with a variance of 0.5:
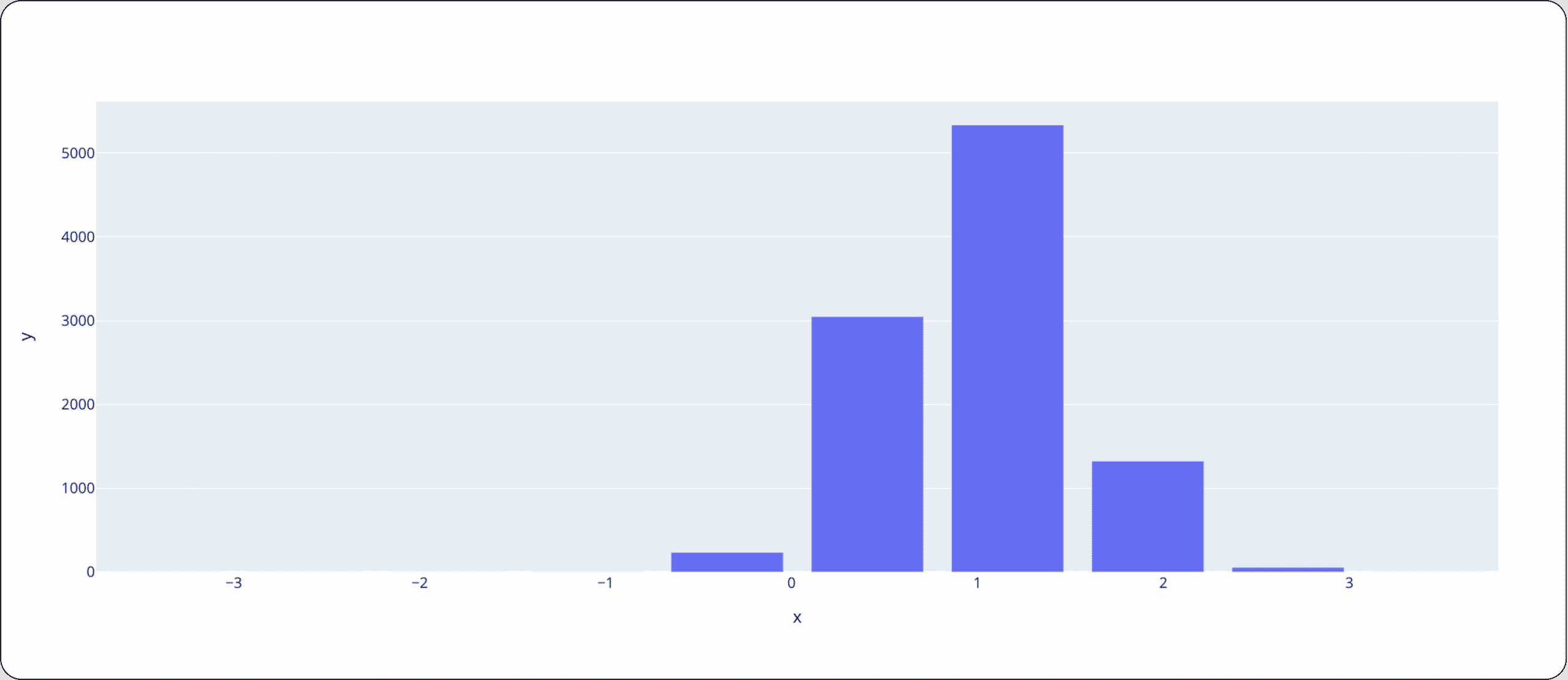
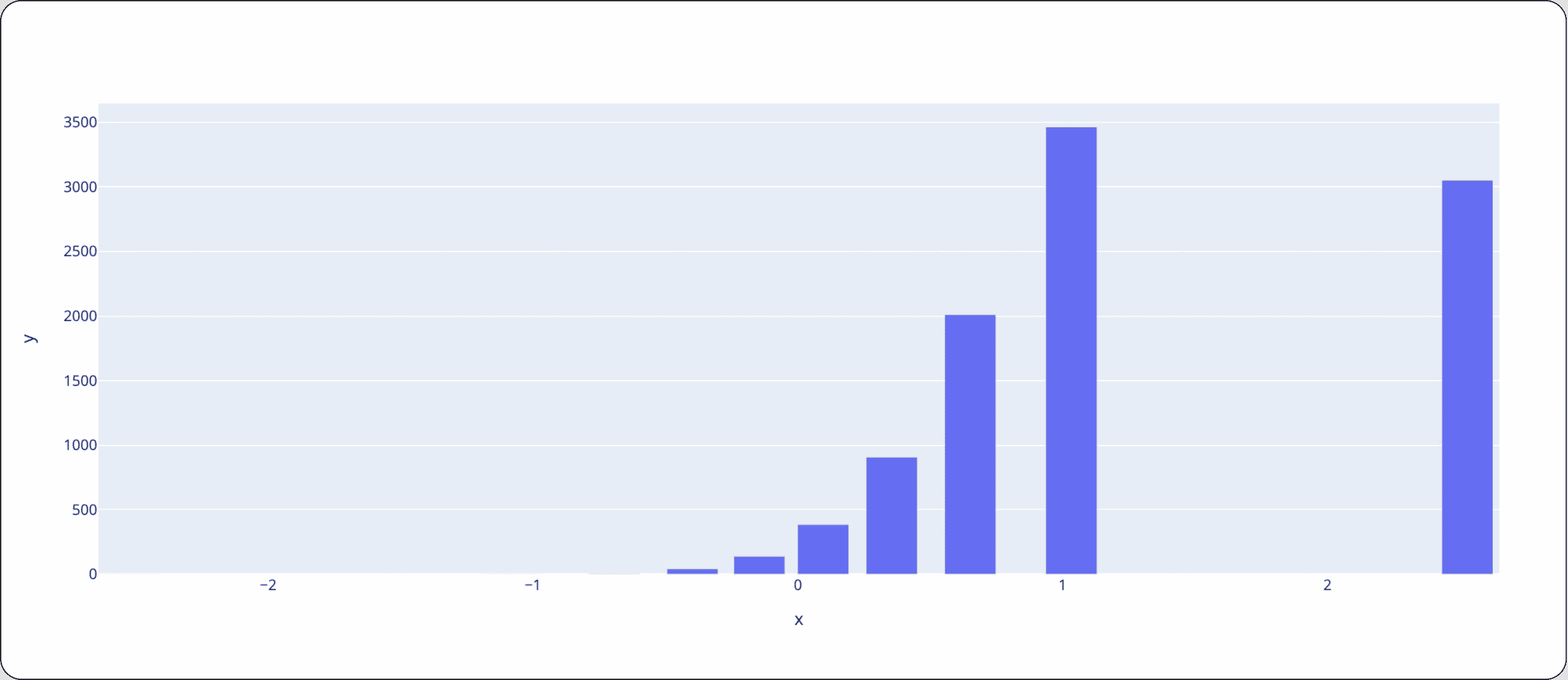
In the experiment, we calculated PSI using 2 different binning strategies (using this code). Below we can see how drastic the change in the result can be even though we compared the same exact distribution but each time with a different binning strategy:

A side note about bins in production
Persisting distribution over large-scale data, an example of which is visualization and monitoring over time, could lead you to persist the distribution in the form of a high-resolution histogram that will only require us to aggregate counters for each bin. Defining the right binning mechanism that enables high-resolution detection of minor distribution changes, covering the entire possible range of the attribute but avoiding having a sparse binning representation, is a challenging task. An interesting approach we have seen by VictoriaMetrics, lets you use fixed bins that, therefore, are always comparable between different timeframes or datasets but also addresses the challenges mentioned above. Please note that the distance between consecutive bins is not the same in this approach, and we haven’t run this experiment with this method (something to look forward to 👀).
5 – Different metrics are sensitive to different kinds of changes
To visualize the drift metric sensitivity to change, we re-ran the same calculations, only with normal distributions where the mean is between 0 and 5, and the variance is between 0 and 5. The following charts show how these metrics behave between normal distributions with various changes in their parameters (difference in mean on the x-axis and difference in variance on the y-axis, and average value by color).
We can observe from the graphs below that:
- PSI and JSD are significantly more impacted by variance difference than mean difference.
- Wasserstein is more affected by mean difference.
- KS encapsulates change in mean and variance by roughly the same magnitudes in this generated example.
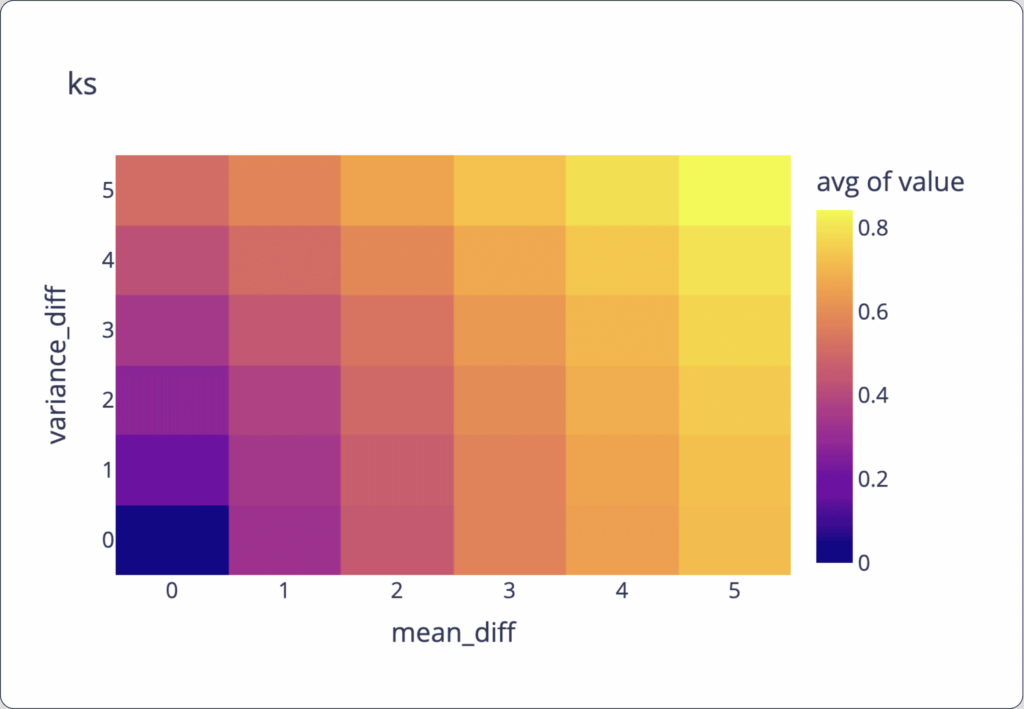
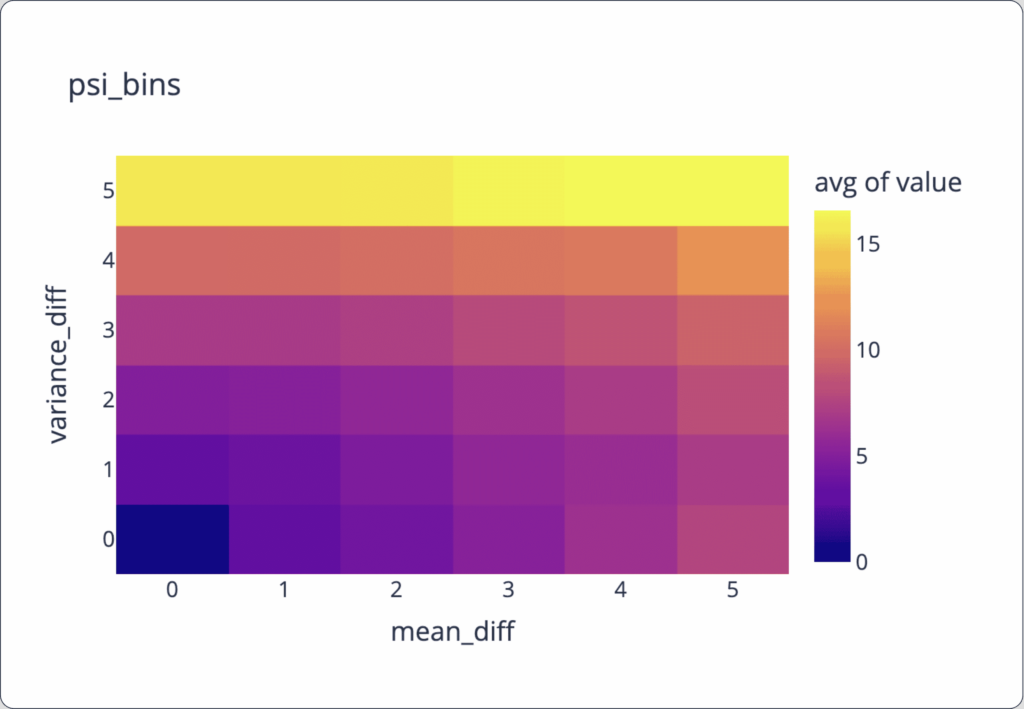
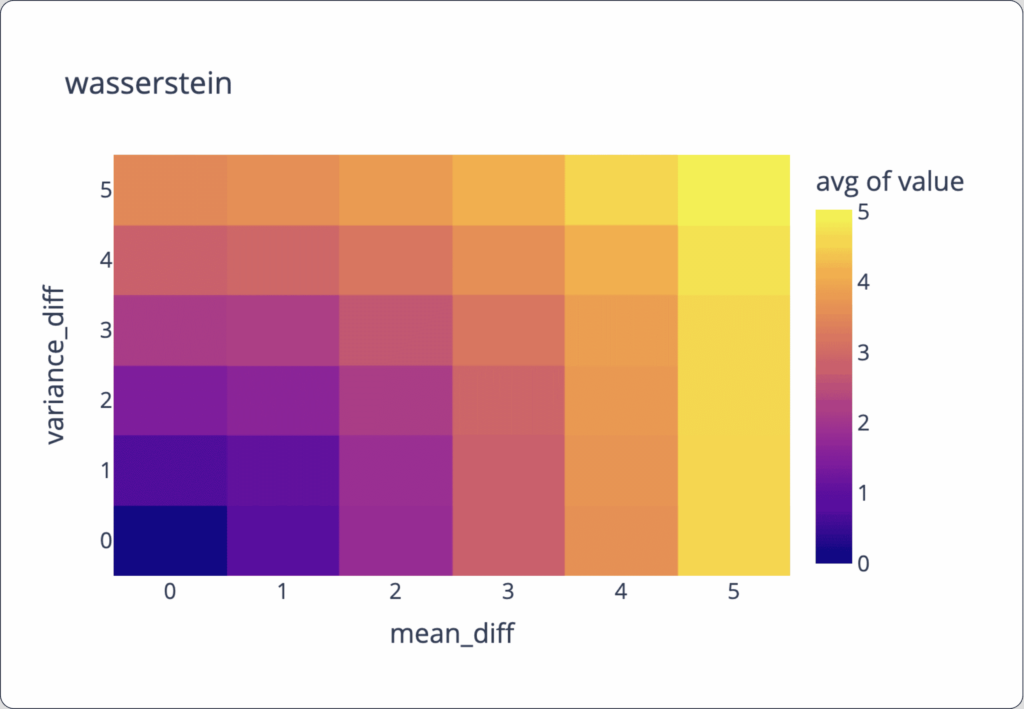
Heatmap that represents the avg level of the distance metric (the color) as a factor of the mean difference and variance difference between two different distributions from the same type
Summary
Measuring drift in production requires that you understand what is the tested period that you want to check, what is the reference distribution that you want to use to compare drift from, and what quantification distance metric you want to use to define the drift distance. This post covered different common distribution distance metrics used for drift analysis. Through a series of empirical tests, we were able to see some of the key characteristics of each one.
One drift metric to rule them all?
As seen, the different drift metrics can be used for different types of attributes. Each metric could have its own scale and sensitivity to different types of change. Understanding scale, sensitivity to change, and the nuances of each metric are important when choosing the appropriate metric/s for your use case. There is no one magic metric to rule them all that could incorporate all nuances altogether.
Measure vs. monitor
Some of these methods are, at their core, tests to get decisive results if drift is present between 2 samples. In a test, you need to set a threshold to determine when drift is present. When monitoring drift over time, a binary answer might make it difficult to understand if a test is too sensitive or not sensitive enough. That’s why measuring drift instead of testing for drift is preferable in scenarios where you are checking for drift over time. This observability approach will indicate the magnitude of the drift without the need to set static thresholds.
Univariate vs. multivariate
For simplicity, in this article, we focused on univariate measures. Some of these same measures have multivariate generalizations as well. In the future, we will cover the topic of multivariate measures and techniques.
The upside to univariate measures is that they are easy to calculate, and it’s relatively easy to pinpoint and drill down into issues on this level. The downside of univariate measures is that you are not measuring drift as part of the joint distribution. As a result, you may miss changes in complex connections between features when analyzing drift.
Want to monitor drift?
Head over to the Superwise platform and get started with drift monitoring for free with our community edition (3 free models!).
Prefer a demo?
Request a demo and our team will show what Superwise can do for your ML and business.
Common drift metrics
In this section, you can find an overview of the common drift metrics and explanations of how they encapsulate drift.
Population Stability Index (PSI)
PSI is a statistical difference that measures the change in two data sets, represented as a single number. It’s essentially a single number that measures how much a data set has shifted over time or between two different samples of data with respect to some feature/label/output.
\[
\quicklatex{color=”#000″ size=25}
\ $PSI:=\left(P_a-P_b\right)\cdot ln\left(\frac{P_a}{P_b}\right)$}
\]
PSI works by binning the records in both sample datasets into comparable bins. The binning strategy can affect the result.
The $ln\left(\frac{P_a}{P_b}\right)$ term works well when a large change resulting from a single feature, which is a good indication of how important the feature is to your model’s behavior. Running this test periodically can help you detect when a change in a feature is impacting your model’s performance. It’s often used in the finance industry because it’s a practical way to measure changes in the volume of data and its categories, for example, when the population of loan applicants changes in a bank.
PSI results are commonly interpreted as follows:
PSI < 0.1: no significant change
PSI < 0.2: moderate change
PSI >= 0.2: significant change
Package/implementation (python)
Kolmogorov-Smirnov (KS)
KS measures the max difference between the CDF of two sampled distributions.
This measure is used in the Kolmogorov Smirnov test in order to check if 2 samples are drawn from the same distribution. Is non-parametric, meaning we don’t need the parameters of the distributions they were drawn from in order to perform the test.
[latexpage] $D_{n,m}=sup_x|F_{1,n}(x)-F_{2.m}(x)|$
where $F_{1,n}(x)$ and $F_{2,m}(x)$ are the empirical distribution function of the first and second samples, respectively, and $sup$ is the supremum function.
Kullback Leibler divergence
Kullback Leibler (KL) divergence, also known as relative entropy, measures how well two distributions match or differ from each other.
[latexpage] $KL\left(Q||P\right)=-\sum_{x}^{}P\left(x\right)\cdot log\left(\frac{Q(x)}{P(x)}\right)$
[latexpage] $KL \in [0,\infty)$
When $KL=0$, it means that the two distributions are identical.
KL is asymmetrical, meaning that $KL(Q||P) \neq KL(P||Q)$ unless they are equal.
If $P(x)$ is high and $Q(x)$ is low, the KL divergence will be high.
If $P(x)$ is low and $Q(x)$ is high, the KL divergence will be high as well but not as much.
If $P(x)$ and $Q(x)$ are similar, then the KL divergence will be lower.
Jensen-Shannon divergence
Jensen-Shannon divergence is a symmetric measure that uses a bounded variant of KL to quantify the difference between two distributions. Because it calculates a normalized score that is symmetrical when using log base 2 for calculating, it is bounded between 0 and 1.
[latexpage] $JSD\left(Q||P\right)=\frac{1}{2}\cdot\left(KL\left(Q||M\right)+KL\left(P||M\right)\right)$
Where $M=\frac{1}{2}\left(P+Q\right)$
Unlike KL divergence, JS always has a finite value.
Package (Note that this calculates the square root of JSD)
Wasserstein distance (Earth-mover distance)
Wasserstein distance, also known as the Earth Mover’s distance, measures the distance between two probability distributions for a given region.
Given 2 sampled distributions binned into n bins, we can compute Earth Mover’s distance as follows:
[latexpage] $EMD_0=0$
$EMD_{i+1}=P_i+EMD_i-Q_i$
$EMD= \sum_{i=0}^{n}\left|EMD_i\right|$
Pearson’s Chi-Square distance
Pearson’s Chi-Square distance used in the Chi-Square test measures whether there is a statistically significant difference between two distributions.
[latexpage] $dist\left(P,Q\right)=\frac{1}{2}\sum_{i}\frac{\left(P\left(i\right)-Q\left(i\right)\right)^2}{P\left(i\right)+Q\left(i\right)}$